分散の加法性（加成性ともいいます）についてきちんと説明するね。ここで学ぶ内容は、標準化の知識とあわせれば、いろいろな平均値の差の検定とか分散分析などの原理を理解するときに役立つはずだよ。分散の加法性の利用には、いくつかの計算事例を知れば、割と簡単に理解できます。

＜分散の加法性の公式＞

 

目的の数値　ｙ　が次のような式でもとめられるとしましょう。たとえば数枚の板の厚み ｘ を合わせたときの全体の厚みが ｙ で表されるようなばあいのことを考えています。これを線形表現の式といいます。   分散の加法性の公式は次のとおりです。   ｘ の分散値（=　標準偏差 2 ）を、 Ｖ[ｘ] のように表現します。これを「　ｘ　の分散の期待値は Ｖ[ｘ] である」と言います。この表現だと、　ｙ　の分散の期待値　 Ｖ[ｙ] は次式となります。 この式は実務的に非常に利用価値のある大事な式です。

《注》

あわせ板の厚みのばらつきを考えるときに、こんな風に考えたことはありませんか？

「ある板の厚みはばらつきのために厚みがうすく、別の板の厚みは厚いことが考えられる。だからあわせ板では、ばらつきがなくなる方向になる」

実はこれは平均値のことを考えています。

あわせ板を作る場合には、厚い板と薄い板が均等に供給されることはなく、確率的に厚い板ばかりの場合もあります。ですから実際に生産されるあわせ板にはばらつきが生じます。しかも一枚の板のときのばらつき巾より、あわせ板のときのほうが厚い板ばかりのケースも生じるのでより広くばらついてしまいます。

平均値では合計計算でばらつきが消えることと、あわせ板の厚みではばらつきが増えることを混乱して考えるひとがいるので説明するね。

板1枚のデータひとつひとつにばらつきがあります。そしてあわせ板の厚みは、あわせた板のデータを合計することで計算できます。このときあわせ板のばらつきは分散（ = 標準偏差² ）を板ごとに積み重ねることになります。これを分散の加法性といいます。
たとえば同じ厚み a　mm であっても納入メーカーが異なる３種類の板を合わせ板にするときには、それぞれの板ごとに標準偏差値が異なります。それぞれ ３種類の異なる分散値をもつからそれをぜんぶ合計した分散値になります。厚みが 3×a mm で計算できるからといっても、ばらつき計算で考える厚みの計算式は、分散ひとつひとつが個別に扱えるように、足し算で表現されていなければいけません。

ひとつひとつにばらつきの性質を持つ「観測値」と、たんなる「係数値」とは分散計算では異なる扱いをしなければいけません。観測値ひとつに対して、ひとつの分散がありますから、分散の加法性の公式を適用するときには、観測値ひとつひとつが別々の変数のように展開されている必要があります。線形に表現された式にしておくことが必要です。

平均値の標準偏差を計算するとき、どのように公式に適用するか考えてみようね。
平均値計算でも、測定値ひとつひとつに分散の期待値がぶら下がっています。でも単に合計しても合計値が算出されるだけで、平均値にはなりませんね。そこで平均値をデータの足し算の形で表現するには、それぞれのデータに重み（係数）をつけたものを足し算します。この重みはひとつのデータには 1/n になりますね。あるひとつの測定値について、重みも２乗になりますから、その測定値の分散値は （1/n）² 倍になります。

分散の加法性の理解には、中学校までの平均値の計算方法からウェート平均計算方法の表現に切り替える必要があります。

分散の加法性の理解のためには、表示されていなくても、「測定値ひとつにはそれぞれ分散がぶら下がっている」と考えることが大事です。ひとつの測定値は最後の計算結果に対してそれぞれどれくらいの重みをもっているかを考えて足し算式（線形表現）にしなければいけません。

あわせ板の厚みのばらつき計算

たとえば、同じ標準偏差 σ を持つ３枚の板をあわせたときにあわせ板全体の厚み ｙ がどれだけばらつくか、標準偏差を計算したいとしましょう。板の厚み　ｙ　の算出式は
　ｙ = ｘ_１ ＋ x₂ ＋ x₃　ですね。
Ｖ[ｘ] = σ ²　ですから、　ｙ　の分散　 Ｖ[ｙ] は次式で算出されます。それぞれの板の係数は　１　ですから、係数は２乗してもやはり　１　です。 　

Ｖ[ｙ] = σ ² ＋ σ ² ＋ σ ²　=　３σ ²

クギ１００本の重量の標準偏差は, もとのクギ重量の標準偏差にたいして　１０倍になることがすぐに理解できます。

トップへ

平均値の標準偏差

平均値にも標準偏差があるぞ。

あなたは毎日同じサンプルを3回ずつ分析しているとしましょう。測定値はばらつきますから、毎日の測定値の平均値もまたばらつきます。
測定値の標準偏差を σ とすれば、平均値の分散 も、分散の加法性の式から導くことができます。

平均値 ｙ は全部の　ｘ₁〜ｘ_n　の測定値を足し算して　ｎ　でわって、算出しますね。だからひとつひとつのデータについて線形表現の次式で書くことができます。

やはりどの ｘ の分散も Ｖ[ｘ] = σ ²　ですから、分散の加法性の式から、平均値の分散（標準偏差 ² ）は次式になります。

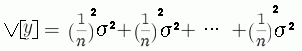
平均値の標準偏差は　1/√ｎ　になりますから、はじめの標準偏差よりばらつきが小さくなります。平均値の標準偏差が　σ/√ｎ　になることを利用して平均値の差の検定などが行われることはご存知かもしれません。

100回の繰り返し測定をしたときの平均値のばらつきは　1/√100　ですから　1/10　になります。有効数字が一桁だけ向上します。もとのデータの正規分布と比較して、平均値の正規分布は　1/√ｎ　だけ狭くなっています。

トップへ

お酒のブレンドとアルコール度のばらつき計算

お酒はいくつかのタンクを仕込んで発酵させます。同じやり方で同じ量だけ仕込んでも、アルコール度にはタンクごとのばらつき σ が出ますから、これをブレンドさせてばらつきを小さくし、品質を安定させます。品質のばらつきを抑えるために、いくつのタンクを混ぜるかは工場設計時に必要な計算です。

ｎ 本のタンクを混ぜると、そのばらつきはどうなるでしょうか。

実は、同じ量だけ混ぜ合わせるときの濃度の算出式は、平均値の算出式と同じになります。ですから、ブレンドしてできるお酒のアルコール濃度のばらつきは　1/√ｎ　になります。

では、タンクごとに混ぜる容量が異なるときはどうすればよいでしょうか？濃度の計算式には、タンクごとに　（タンク容量）/（合計容量）　の係数がかかりますね。あとは公式に当てはめて計算するだけです。

ここで、注意すべきなのは、最初に立てる式は、カッコでくくったり、方程式の演算を加えてはいけないということです。平均値の計算式は、まず合計して、ｎで割ることが通常の計算方法ですが、分散の加法性を適用するときには、ひとつひとつの変数に係数（ウェート）がかかった形の式からはじめなければいけません。これを、線形表現された式といいます。

たとえば、１００本のクギ重量は、１００×（１本のクギ重量）の式ではなく、１００の変数が足し算で表現された式となります。

トップへ

 本文に戻る

本文の「ばらつきの四則演算の応用計算」をあわせて読んでもらうと分散の加法性全体が見えやすいと思います。