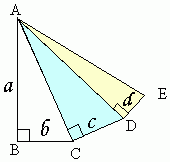第8章 中級
標準化、共分散、相関係数の
意味を知ろう

• サーチエンジンから直接入ってきた人は、フレームで目次を示していますからこれで目次表示にするとタコ国全体が見やすいです。目次からここへは 8 章から入ります。
• 自由度とは何かを知りたいかたは（おまけ）へ。イラストでの説明だよ。
• 「共分散とは」何かを知りたければこのイラストをじっとよくみて下さいね。

 

標準化とは

標準正規分布って何？

標準偏差とはデータの群があるときその「ばらつき」の指標です。 平均値があるようなデータ群の場合には、データｘを横軸に、そのデータの出現頻度を縦軸にすると、下の図のようにベル型の正規分布をします。平均値を中心にして含まれるデータ数が６８％になるときの、平均値からのｘの値（差分σ）を標準偏差といいます。 正規分布は、データ群によっていろいろな形があります。単位によっても分布の形状は変わります。たとえば、同じ物をはかっても長さをcmとmmと表した場合では異なる正規分布形状になります。 データを平均値をゼロにした比率尺度に変換して正規分布をつくれば、すべてのデータ群から 平均値＝0、標準偏差＝1 である同じ正規分布の形状へと変換することができます。 　 標準偏差の意味と計算）・・・・再クリックで閉じる データにはひとつひとつばらつきの情報量があります。全体のばらつきの情報量の総和が平方和ですが、データ数で割るとデータひとつあたりのばらつき情報量の平均値が算出されます。標準偏差はその平均情報量の平方根値になります。 自由度で平均することが理解できない人は、下のほうに「n − 1 で割り算して標準偏差を計算する理由」で説明しています。 エクセルで標準偏差だけ計算するのは簡単。関数STDEV( )　を使う。 C4からC8にデータが並んでいれば次の式をセルに書けば値が出ます。 試料標準偏差です。Standard Deviationという意味です。 =STDEV(C4:C8) 別にわざわざ関数式を作らなくても神田さんのソフトを実行すれば、必要の有無にかかわらず、平均値と標準偏差、相関係数などセットで算出されます。平均値の関数は =AVERAGE(C4:C8) だよ。 統計処理を勉強すると、母集団・正規分布・標準化などという言葉が頻繁に出てきます。母集団とはある共通の特徴をもつ対象のことで、いまの人たちにはドメインだよといった方がわかりがいいかな。動物界の中の人間、会社内の庶務課の人間とかいろいろな切り口がある。 その母集団からデータを取って、ヒストグラムを作るとベル型の分布をするときには、無限のデータでは正規分布する。 　 エクセルでヒストグラム作成）・・・・再クリックで閉じる エクセルでヒストグラムを作りたければ次の手順でやってね。 データ範囲を選択・反転＞ツール＞分析ツール＞ヒストグラム＞ＯＫ＞新規または次のワークシートにチェック、グラフ作成にチェック＞ＯＫ＞どれかの棒グラフの棒の中で右クリック＞データ系列の書式設定＞オプションのタブ選択＞棒の間隔スケールバーを０にする＞ＯＫ これで自動的にデータ区間を割り振ったヒストグラムができるよ。ヘルプボタンで詳しいマニュアルが出ます。自動がいやなら巾指定もできる。ほかにいろいろ指定できます。パレート図、累積度数分布のグラフ、ヒストグラムのグラフ作成などできますね。 ヒストグラムは一般の棒グラフのように棒と棒の間に隙間をあけて表現してはいけません。密着させることで連続数であることを表現します。 正規分布をベル型の曲線で表すのは連続数だからです。ポアソン分布は数の間の横軸に数値の意味がないから、隣の棒とつなぐ線の意味は、本当はありません。ただ、同じようにベル型に近いよというメッセージを伝えようとするときには破線などで曲線を示すことがあります。 離散数（ 1.672 とかでなく１〜２，13〜14　などの間に数がはいらない数）の場合は、ヒストグラムを作れません。無理に作ると、規則的に凸凹のあるヒストグラムが出来上がります。区間間隔が離散間隔の倍数であれば分布の形状には意味が出てきます。 理屈だけでいうと離散数では、間に数がないからグラフを巾のある柱で表すのは本当はいけません。それではグラフとして見栄えもわるいから、柱どうしが離れている状態で表します。連続数のヒストグラムは柱の巾もぴったり隣の柱にくっつけて表すのが正式です。連続数では横軸のどの部分にも数としての意味があるでしょ。 離散数は棒線で表します。離散数の出現頻度は正規分布とは呼ばずにポアソン分布などといいます。 　 エクセルで正規分布曲線作成）・・再クリックで閉じる 正規分布の絵を描きたいけれどエクセルの関数には累積関数しかないため、正規分布曲線がかけないと嘆いている方へ。 関数式を作ればできるぞ。 一般の正規分布の確率密度関数の場合   元データｘ値はエクセルのセル B4 〜 B20 に記載されているとしよう。 B1 には平均値、 B2 には試料標準偏差が入っているとしよう。 次の式をコピーして、 C4 セルへ貼り付けよう。エクセルに貼り付けるとき書式が乱れることがある。一度関係のないセルに貼り付けてから、再度数式バーからコピーしなおして C4 セルに貼り付けると良いぞ。後はドラッグして貼り付けるだけ。 =EXP(((B4-$B$1)/$B$2)^2/2*-1)/$B$2*SQRT(2*PI()) 標準正規分布の場合 標準正規分布の確率密度関数は μ が 0 、σ が 1 だから次式のように簡単になる。このときの ｘ は標準化したＺ値だから間違えないように。Ｚ値とは海外で使われている表記で、日本の教科書ではｘでなく u 値と表現していることが多い。エクセルがＺ値といっているので、最近はＺでいう人が多いかな。   セル F4 以降にＺ値がはいっているとしよう。−4〜+4の範囲で0.5刻みじゅうぶんです。となりのG4に次の式（そのＺ値にたいする確率密度の算出値）をコピーしていれよう。 ここで、分母の定数は２πの平方根です。 =EXP(F4^2/2*-1)/2.506628 エクセルのグラフ作成 x 値（またはＺ値）と確率密度の数値領域選択＞グラフアイコン＞グラフウイザードで散布図選択＞プロットのない曲線表示選択＞完了　     （別法）エクセルの関数を使って確率密度を計算するやり方 次の関数式をB1に入れれば、A1にあるZ値の値を参照して、B1のセルにその確率密度を表示します。 ただし平均値が０、標準偏差が１の標準正規分布の確率密度です。TRUEにすると片側確率の値（分布関数値）となります。 =NORMDIST(A1,0,1,False) 真中に平均値があることは知っているだろ？正規分布の特徴は、標準偏差を σ （シグマ）とすると、平均値を中心にしてほぼ±３σの範囲内にデータが入ってしまう性質がある。 標準偏差の １−２−３ に対応した 68 − 95 − 99.7%という数値は実社会でも使うから覚えておく必要があります。 むしろ、この外側にあたる、 32− 5− 0.3 ％を覚える必要があります、といったほうがいいかな。よく報告で書いてある「危険率５％で差があります」などという表現は２σのときの数値ですから。 正規分布を数式的に表現すると次のように表されます。慣れると毎回言葉で説明されるよりわかりやすいよ。 N は 正規分布 Normal disturibution の頭文字だ。標準偏差を二乗表示するのは、分散という意味で二乗にしてある。この位置に書く値が分散値だったら、二乗にはしないからね。 N ( 平均値，標準偏差２ ) 平均値をμ（ミュー）とすると次のように書かれるわけだ。平均値と標準偏差には単位があることに注意しておいてね。たとえば、ある学級の子供達の身長をcm単位で書いたデータと、mm単位で書いたデータでは、同じ子供達の身長であっても平均値も標準偏差もちがう正規分布になります。 N ( μ , σ2　) ただ、このままでは、分布の横軸には単位があるから、その後の計算をするのに、データを取るごとに毎回、正規分布確率密度関数式というものを作り直して計算してゆかなくてはならなくなる。とっても扱いが面倒。そこで出てくるのが標準化（または基準化）といわれる換算方法なのだよ。 標準化とはいろいろな単位で扱われている正規分布を、単位のない無次元数に変換し、平均値が 0 、標準偏差が 1 である次の正規分布にする計算方法のことを言っている。標準化して算出された値をＺ値とよぶ人もいる。 ひとつひとつのデータを次の標準化の式で換算しなおして出来てくる比率データの正規分布だよ。このＺ値の正規分布は一種類しかないんだ。この換算式さえ知っていれば、扱いを共通化できるので、一種類の確率密度関数とその表類を準備しさえすればよく、大幅に手間が省けて便利になる。この換算後の正規分布を標準正規分布といいます。くりかえすけど、標準正規分布には単位がありません。 N ( 0 , 12 )　　　　　　　･････ 標準正規分布　 　　 ･････　標準化の式（ 標準偏差を 1 とした比率の値 。Ｚ値ともいう。） ここでは、データの順番 i として、 i 番目のデータを xi と表現すると、換算した後の xi に対応するデータ（Ｚ値）を ui とする。ui は比率となって単位が消えています。それぞれのデータの偏差を標準偏差との比率とすることで無次元化しました。ui は、ばらつきを比率にした数値だね。標準化とはばらつきを比率にする計算作業のことです。 あるデータのばらつきは標準偏差の何倍であるかということがわかります。 2 倍以上のばらつきになる頻度は全体で５％くらいしかありません。 標準化したばらつきが 2 以上あるデータが出たときに、あなたがこのデータはいつもと違うといったら、100 回判断したら 5 回くらいはいつものデータである場合があるわけです。あなたが判断ミスをする確率は５％ですね。それで報告には「危険率５％で差があると判断する」という表現をします。 標準化することをルール化しておけば、ばらつきが 2 以上かどうかだけ判断すればよくなるので便利です。 　  Z 値と危険率 α 表）・・・・再クリックで閉じる エクセルの関数でＺ値から危険率の計算ができます。セル内に次の関数を書けば片側危険率が表示されます。（）内の数値は標準正規分布　Ｎ（０，１2）のＸ軸の値です。この例では２σの片側数値が求められます。両側の危険率はこの数値を２倍すればいいですね。 Ｚ→片側危険率α =NORMSDIST(2) Z 値   両側検定 片側検定 危険率       0.1 1.64 1.28 0.05 1.96 1.64 0.01 2.58 2.33 0.001 3.29 3.08  主成分スコアの分布は？ ここは、主成分層別法をやってみた人向けの説明です。初めての人はとばして下さいね。 　  学びたい人　　More 》・・・・再クリックで閉じる   相関係数による主成分分析で算出される主成分スコアは標準化（無次元化）された偏差（ベクトル）を回転座標の中から見た数値になっています。 分布に偏りがないと仮定する場合には、主成分スコアもまた標準正規分布になりますから、主成分スコア1以下となるデータを、あまり主成分特徴のないデータ群として扱う目安に利用できます。主成分層別法は標準偏差１を境にして関係が強いか、そうでないかを分けようとする考え方をとっています。 ある主成分について、正規分布の外側にあたるデータの３２％ほどを主成分特徴を有するデータとして扱うことにしているわけです。 実際にはデータ分布には偏りがあるので、全ての主成分の特徴をもたない６８％にあたるデータ群は、変数ごとに偏り分だけ主成分の特徴があるデータに分類されてゆくケースが多いと思われますから、６８％よりもっと少ない割合になるでしょう。 主成分層別の切り分けの数値 1 は、たとえば人により 1 より小さい値が選択されてもなんら問題はありません。抽出されたデータの散布図などから情報を取り出すときに判断をまちがわない何らかの根拠があればよいのです。 たとえば、楕円形の分布を仮定すればマハラノビス汎距離をつかうとか、いろいろな考え方は出てくるでしょう。どうぞチャレンジしてより良い方法を見出してください。 私としては、そもそもどのような分布形状かわからないデータをまずとりあえず扱ってゆく方法としては、この程度のラフさでじゅうぶんではないかと考えています。 ラフではあっても、分類データや順位データなどを同時に扱える環境のメリットの方が大きいと考えます。 区切り目を示さず主成分スコアの大小を論じる立場は、大小の区切り目を示して議論するより、もっとあいまいな立場での議論方法です。区切りの数値根拠を示さずに、主成分層別法はいけないだのという人は、議論をしているのではなく、気に入らないといっているだけですから聞き流すように。 ある主成分の性質を論じるととしましょう。 主成分スコアから何も情報を得ないで主成分分析したとするやり方 生データのうち、どれをより主成分特徴のあるものとコンピューターは判断したかを主成分スコアから知るやり方 ２のほうが、よりずっと優れた方法です。 ２は実際の分布を見ようとする態度、１は実際の分布は関係なく主成分は直線であると仮定して議論する態度との違いが生じてしまいます。

母平均と試料平均、ならびに母標準偏差と試料標準偏差

統計を勉強してまず引っかかるのが、標準偏差を計算するのにいきなり　n − 1 という自由度で割り算しなさいという説明に出くわすときである。 で自由度って何？という話になる。しかもそこで出てくる値には不偏分散という名前が出てくる。不偏と辞書で引くと偏りのないという意味だということがわかるだけ。何かよくわからないうちに、毎回計算するから慣れてきて疑問を抱かなくなって卒業となる。 平方和を平均するのになぜ n ではなく、 n − 1 になるのか。それを明らかにしておこうね。

自由度とは　･･･　( n − 1 ) で割り算して標準偏差を計算する理由

右図は　N ( μ , σ2 )というある母集団から試料を取り、試料データから　というヒストグラムが得られたときの二つの分布を並べています。 この章でつかう言葉の定義をしておきますが、右図の矢印の長さを「効果」といいます。 実験して観測されたデータの大きさを実験効果と呼ぶ意味での効果です。効果にはプラスとマイナスの効果があります。 効果の二乗値は「情報量」と呼びます。 沢山あるデータの中の、右図の赤い〇で示される位置の「ある一つのデータ」について考えます。 試料の分布では試料平均値を使ってばらつき計算するから、平方和は a の効果分で計算されることになります。 本来のばらつきを知るには真の平均 μ から計算しなければいけませんから、 b の効果分で平方和を計算しないといけません。試料平均値で計算していくと、算出される平方和には常に Δd 分の情報量が減少していることになります。 標準偏差は「ばらつきの平均値」的な意味を持つ数値ですが、計算は二乗値（＝平方値、すなわち情報量）で行います。ひとつひとつのデータの平方値の平均値が分散で、その平方根が標準偏差です。データから母平均を差し引いた 真のばらつき効果 b で計算した平方和を分散値に計算するには、データ数 n で割り算することで平均します。 試料平均値はすぐに計算できますが、母平均はわかっていないのが普通です。だから、仕方なく母平均の代わりに試料平均値を使ってばらつき計算します。 ところが試料平均で算出した平方和には平均値のずれ分の情報量が含まれていないため n で割り算すると平均値のずれ分だけ推定結果が小さくなりすぎます。 この平均値のずれ部分の効果を考慮すると、理論的には　n − 1 で割り算すると偏りのない分散値が計算できることが証明されています。 　（ 証明　）・・・・再クリックで閉じる   ( 証明 ) １　方針 偏差の二乗値（分散）の期待値を求める。 次に、分散を足し算して平方和を求め、それが ( n − 1 )σ2　となれば、証明終わり。 ２　分散の期待値を求める 偏差を母平均からの差に書き換える。母平均からの　データ X の分散の期待値は　σ2　、また母平均からの　平均値の分散の期待値は σ2 ／n である。 ３　平方和の期待値 X i の i = 1,2,3,･･････，n　について分散の総和が平方和である。 証明終わり。 このデータ一つあたりの平均的ばらつきの平方値を、偏りのない分散ということで不偏分散とよび、日本では通常　V　と表現されます。 V の平方根を試料標準偏差と呼びます。一方、真の標準偏差を母標準偏差とよんだり、単に標準偏差とよんだりします。 この「母」とか「試料」という概念は、平均値の差の検定など他の様々な統計手法を、どれを適用したらよいか判断するとき重要な知識になります。試料の代わりに標本と使う人もいます。 まだわからんという人のために　（おまけ） イラストでわかる自由度と不偏分散　を補講としてつけました。これでもわからんのなら、あきらめてくれ。 行列計算できる人用の説明としては、自由度とはランク数のことで、平均値を利用したことでランクを一つ消費したことになります。

分散の意味、共分散の意味

上の図では「 a はバラツキである」と直感的に理解しやすいのですが、計算の世界ではその効果をそのまま四則演算してもばらつきの計算は出来ません。 データのばらつきを全部そのまま足し算するとどうなるか知ってますか？ゼロになるよね。この性質を利用して、ばらつきの効果を消す目的で合計します。これが平均値が求められる原理です。合計するという行為は、データからばらつきの情報を消すために行われるのです。 ここでばらつきの計算をもういちど見直してみようね。

ばらつきの四則演算

ばらつきを四則演算するには、二乗（または平方）の値で行われるということを知っておかなければいけません。効果の四則演算は、情報量（二乗）で行われます。 データがばらつくということは多数のコントロールできない因子の微小な効果分がデータの大きさに影響させているためにばらつくのです。 右図は、例としてデータに影響を与える4種類の因子がどのように標準偏差に影響するかを図示したものです。 4種類の因子の与える影響の効果を a 、 b 、 c 、 d の大きさとします。効果 a に、 b の因子によりばらつきが増えるとすると、 　a2 ＋ b2 の値、すなわちピタゴラスの定理でAC2 になります。すなわち a 、 b のばらつきが合わさると AC の効果の大きさでデータがばらつくのです。同じように、 a 、 b 、 c の効果が合わさってばらつきになれば、AD の効果になるのです。 a 、 b 、 c 、 d なら AE が4種のばらつき要因が重なったときに観測される標準偏差になるわけです。 効果はマイナスにも作用しますので、観測データは平均値に対してプラスとマイナスの両方に分布しますから正規分布になります。しかし、ばらつき因子が増えると、標準偏差は増加する方向にしかならないことがこのピタゴラスの定理の連続の絵で理解していただけると思います。 多変量解析が、普通の分散分析と何か違う特別のものと考えている方もいると思いますが、情報量で取り扱うやり方が変わっているわけではありません。取り扱う変数の数が多くなっただけです。 この世の中は二乗の世界でデータが見えているのです。ピタゴラスの定理の連続がばらつきの世界でもあります。物質の原子構造はデジタルの世界ですが、現実の社会で観測されるデータでは、無数のばらつき要因が重なった結果なので、いろいろの観測値が定量値として連続したように見えるわけです。   ばらつきの四則演算の応用計算　 　 　 −−　分散の加法性　計算例　−− 分散の加法性（加成性）の公式と説明 （設問） トランプの箱を設計したい。トランプの厚みの分布はmm単位で N( 0.5 , 0.012 )である。トランプにはジョーカー2枚入れて全部で54枚をひとつの箱に入れる。54枚重ねたときの厚みに、標準偏差の3倍を余裕しろとしてスペースを空ける。箱の厚みはいくらにすればよいか。 （ 興味があれば見て　）・・・・再クリックで閉じる （計算） ばらつきが54枚分重なるから、全部重ねたときの厚みの分散は次のように計算される。 分散 = 0.012 ＋　0.012 ＋　・・・・・ ＋　0.012 （54個の足し算） 　　 = 54 × 0.012 　　 = 0.0054 = 0.07352 トランプセットの厚みの分布は次のとおり。 N( 0.5 × 54 , 0.07352) 3σ = 3 × 0.0735 = 0.221 mm よって 箱の厚み = 0.5 × 54 ＋ 0.221 = 27.221 mm 分散が足し算されるという性質を分散の加法性といいます。実務性の高い性質です。たとえば、1000本入ったくぎの総重量をばらつきをいれて考えるとか、平均値のばらつきはいくらになるのかとか、3本のタンクの溶液を混ぜると濃度のばらつきはどれくらいになるかとかいった利用法が実際に使われています。 分散の期待値を V( x ) と表現しよう。ばらつきのある変数 X , Y の分布は次であったとする。 N ( X ,σx2　)　、　N( Y , σy2　) 次の計算式で算出される値のばらつきはいくらになるか。 X ＋ Y →　V( X ＋ Y ) = σx2 ＋ σy2 X − Y →　V( X − Y ) = σx2 ＋ σy2 引き算でも分散は足し算ですね。間違いではないんですよ。平均値が増える方向でも減る方向でもばらつきはそれまでより増えるという性質です。 ただし、映写機のフィルムの大きさのばらつきとスクリーンに映る画面のばらつきは相似計算になるため上記の式は当てはまらないから注意してください。 カードの厚み場合は、一枚のカードのばらつきが拡大されるわけじゃないから足し算です。映写機では画面上の枠長のばらつきは拡大比率に従って拡大されるから掛け算になります。掛け算の式は要注意ということです。   じゃあトランプから10枚カードをとったときはばらつきが増えるの？という疑問が出ます。 ばらつきは減ります。なぜなら、44枚分のばらつきを計算するのと同じだからです。 引き算のばらつきが増えるというときは次のようなケースと考えてください。 3枚のうすい木の板を製造して張り合わせ、最後に厚みを調整するときに２回に分けて板を削ったときにそのばらつきはどうなるか？という問題です。 板の厚みのばらつきと、張り合わせのばらつきが加算されます。最後に、切削のばらつきが加算されるのです。 数式だけからばらつきを考えてはいけません。実際の作業の中でばらつきの計算は決まります。 ３+３+３＋３＝１２　と　３×４＝１２　という計算はばらつきの計算をする上では異なる意味を持っています。   標準偏差とは 母集団を決めると平均値が決まります。 母集団を決めるということは、管理できる 同一条件の因子 と ばらつきの因子とを区別することです。同一条件の効果はばらつきませんから、データを合計しても消えません。いっぽう管理できていないことから起こるばらつきの効果は合計するとゼロとなり、ばらつき効果を消すことができます。 （重要）データを足し算すれば平均値の情報だけになります。 データを全部足し算すると、（平均値×ｎ）の数値になりますね。これは、データを全部足し算すると、 ばらつき合計＝０ となることと同じことを意味しています。繰り返して言うぞ。データを合計するとばらつきの情報は消えてしまいます。 （重要）平均値が算出できるからデータとの引き算で偏差が計算できます。 偏差とは管理できない、その他の無数の因子群がつくる効果のことを言います。管理できないからばらつきます。管理できるほうは平均値です。偏差の２乗は、データひとつのもつばらつきの情報量でしたね。で、全データの偏差の情報量を平均して一つのデータあたりの情報量としたのが分散ということです。 分散の平方根が標準偏差だね。だから、標準偏差とはばらつきの効果の平均的なおおきさであるといえます。 標準偏差とは何かを知るため同じことを視覚的（四角的？）に説明しよう。 Ｑ：　いろいろな大きさの正方形があります。この平均的な面積の正方形をどうやって描けばいい？ Ａ:　全部の面積を合計して平均値を出し、その平方根を一辺とする正方形を書けばいいね。 標準偏差を計算する考え方はこれとおなじです。 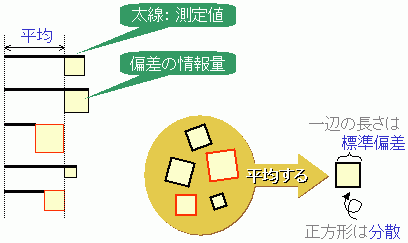いま、偏差の大きさ（＝個々のデータのばらつきの効果）を一辺とする正方形を考えます。すべてのデータは、いろいろな大きさの正方形を持っています。 正方形の面積は２乗した値だからばらつきの情報量の値になります。いろいろな大きさの正方形の平均的な面積をもつ正方形が考えられますね。この平均的な正方形の面積が分散で、そのときの正方形の一辺の長さ（＝ばらつきの効果）が標準偏差です。 全部の正方形の面積を足し算したものが、平方和 S （または総分散）です。真の平均値から算出した平方和なら、平均するときにデータ数 ｎ で割り算すれば平均の分散は算出できます。 エクセルの関数で、平方根は　=SQRT（セル参照）で算出します。 または fx(関数貼り付け)ボタン＞数学／三角＞SQRT＞セル参照 または数値入力＞ＯＫ しかし上の自由度のところで説明したように、通常は試料からえられた平均値は真の平均値（母平均とも呼ぶ）からずれたものが得られます。通常は、測定値は全体の一部を測定するだけですから、試料平均値で算出された平方和は、真の平方和より平均値のずれ分だけ小さいものが算出されます。だから、平均するとき、データ数ｎで割り算せずに、平均のずれ効果分の１だけ小さい自由度 （n-1） で割り算することで、真の分散の推定値を算出します。自由度で算出した分散値は偏りがないため、不偏分散と呼びます。自分がどちらの平均値を使っているかで適用する統計手法が異なってきますから、次の対応関係をよくにらんで覚えていてください。 母平均　　母分散　　　正規分布　Ｚ（または u ）値 試料平均　不偏分散　　ｔ分布　　ｔ値 統計手法では「母平均が既知のばあい」と「未知のばあい」とで違うのですが、「未知のばあい」は下側の試料平均の対応関係の標準化の式や表を使って行います。   通常の四則演算は母集団の平均値を決める 観測している同一条件下で２個以上のくり返しデータを取れば、管理できる平均値の情報量と、管理できないばらつき情報量が分離できます。 平均値とばらつきを分けるためには n = 2 、すなわち繰り返し試験をしないとばらつきは分離できない。繰り返しのない試験を数多くするより、繰り返し数が２であっても繰り返しのある試験のほうが早く真実に近づけることを知っていようね。日による変動も検出するには何日か日を変えて繰り返し実験をする。すなわち統計では繰り返しのある２元配置実験をすれば日による変動も分離できる。繰り返しのない試験を長くだらだら続けて何も結果が出ないより、集中的にやれば一発で方向を決定できるぞ。 観測している同一条件下での平均値は、母集団を設定すると決まってしまいます。母集団をあいまいにすると平均値の情報量と、分散の情報量があいまいになり測定結果も信用できないものになります。適当に拾ってきたデータから平均値や分散を計算してもあまり意味のある行為ではありません。 母集団のばらつき因子のなかに管理できる因子を発見して二つの母集団に分けるとどうなるでしょう。この作業を層別といいます。みんな知っているあの層別です。新しい二つの母集団に今までばらつき因子だった効果分がこれまでの平均値に加算されてそれぞれ別の平均値が出来ますね。同時に今までのばらつき因子から層別因子の効果分が減って標準偏差が小さくなります。 （注） 層別とは管理条件を一つ厳しくした母集団を作ることですから、それぞれの集団で新しい因子分だけ平均値が変わります。同時にばらつきはその因子一つ分だけ減少することになります。統計処理初心者は、こういう「どれが管理されているか」の視点で、２元配置分散分析の意味、繰り返しの意味などを考えると、他の統計処理全体の統一的な理解が早まりますよ。 小さくなったばらつきで平均値を比較する方が判断精度は良くなりますね。「分けることは知ること」と言った人がいます。分類整理する作業は、単純労働ではなく混沌からダイヤモンドを発見する方法なのです。 直感でよいから違う部分を見出し、層別して集計するという作業があたらしい視点を提示できるし、外部に発表できるような仕事ができる方法でもあるのです。  （ランダムと意図）・・・・再クリックで閉じる 統計処理を勉強すると、サンプルはランダムにとりなさいとか、テストの順番はランダムにしなさいというふうに教えてもらったはずだね。 その意味は、ランダムにサンプルを取らないと別の母集団が出来上がるということなんだ。層別と同じことがおこる。ある種の機械の性能を調べたいとしよう。機械Ａと機械Ｂがあるとき、機械Ａの製品ばかりサンプリングすれば、結果の平均値には機械Ａの効果を含んだ偏った性能をしらべていることになります。 試食のテストをするとき、はじめに試食するときは空腹で美味しく感じられるが、後のほうになると飽きてしまって、普通の味だと感じるようになる。試食順序によって効果がかなり異なる。パネリスト全員に同じ順序で試食させると、はじめのほうで試食したテスト品が良い結果になる。 こうしたことを利用して組織内でサギ行為をする人も多い。統計でウソをつく人たちだ。母集団をはっきり意識することは、君がうそつきになるかならないかを決めるくらいの重要なことなんだよ。 社会ではデータがないと、どんなに良いことを言っても根拠がうすく感じられるため、口先だけの人になってしまいます。 逆に、組織内で統計数値を出して議論を進められると、何も検討せずに出席した人たちは反論しにくい。当然、資料を提出した人たちの思い通りにことが運ばれる。これを理論武装という。 企画部門の権力維持につかわれる定番の方法だけど、タコ国で勉強する君達はそんなことをしてはいけない。フェアでないと国や会社が疲弊するぞ。フェアを主張するあまり、一人で集団に対決するとつぶされるから気をつけてね。フェアな態度で再現性のある統計資料を作成することが、発言力と人望を兼ね備えることのできる方法です。 主成分分析にカテゴリー因子を入れることで、管理できる因子とそうでない因子を計算機で見つけることができます。世の中でデータマイニングといっている作業は主成分分析を使えば機械的にやれる作業に変わります。 タコでもわかる主成分分析で、積極的にカテゴリー変数を取り入れる理由はここにあります。データを見分けるセンスのないタコ人も出来るようにしたダイヤモンドを機械的に発見する方法なのです。   ちょっと視点を変えて、平均値も情報量の効果であるという話 上の図で、 a の因子を管理化して母集団とすれば AB が平均値となります。 AB2 が平均値の情報量であれば、 AE が b 、 c 、 d のばらつきを含めた観測値ということになります。 データ2合計 = 平均値2合計 ＋ ばらつき2合計 　 このことを知っていれば、主成分分析で固有値が全体の情報の何％を回収したとか、回帰分析では決定係数から回帰が何％の情報を説明している等といった意味がわかるはずです。   主成分分析と因子分析の宗教論争は止めようね 「主成分分析は、ばらつきを考慮していないため分析法としては劣っている」という言い方をする人がいます。 ここまで学んできた人は、平均値とばらつきとは、合計という操作で情報量を切り分けたことを知っています。主成分分析は、軸の回転という方法で主成分スコアとそれ以外の情報量を切り分けた方法です。それ以外の情報量とは、主成分的にはばらつきに近い概念を持つ情報量です。 いずれも、情報量を２乗であつかう方法です。情報量の切り分けの考え方が異なるだけですから、その考え方の論議なしに、「主成分分析は母数の考え方が無いからダメだ」という議論は、軸を回転させることはいけないと主張していることになります。 情報量の考え方でなぜ測定値は正規分布をするかを理解していれば、このような議論はなくなるはずです。恥ずかしいし・・・。

分散・共分散

データを X とすれば、ここでは平方和を Sxx と表しておきましょう。同じようにデータ Y とすれば、その平方和を　Syyとしておきます。すると分散は次のようになりますね。通常不偏分散は s 2 と小文字の英字で表現されることが多いですが、ここでは平方和と明快に区別するため、varianceの V を採用してVxx 、 Vyy と表現しましょう。添え字の xx というのは X ばらつき効果を二乗して情報量にしたということを示しています。 Vxx = Sxx／(n−1) Vyy = Syy／(n−1) 分散　V 値とは標準偏差の平方値の推定値なのです。分散とは偏差情報量の平均値です。分散 Vxx は X 方向だけでばらつきを計算しているため、 Y とは直接関係のない数値です。 Vyy についても同じです。 X とは関係なく話が済んでいます。互いに関係ない世界です。   いよいよ共分散の話にうつります。データから平均値を差しひいた値が偏差でしたね。 X の偏差と Y の偏差との積を偏差積といいます。偏差積を全部足し算したものを偏差積和 Sxy といいます。Sxy をデータ数で割った偏差積の平均値を、共分散といいます。cov(x,y)などと表現されますがここでは Vxy と表すことにしましょう。母平均から計算された真の偏差積和なら次式で計算されます。 Vxy = Sxy／n 試料平均値から共分散を計算するには、分散の計算と同じように n − 1 で割り算するのが不偏推定値となります。 Vxy = Sxy／( n − 1 ) 偏差積和 Sxy 、 共分散 Vxy って何を意味するのかを勉強してみよう。分散や平方和は二乗だから必ず正の値です（右図参照）。 右図には共分散の意味を座標で示しています。図中に示されているように、共分散はｘとｙの各データから平均値を引いた値（偏差値）の積です。 その積の値は ( x , y ) のデータがそれぞれ平均値より大きければ、重心（ｘ，ｙの平均値）を原点にした座標軸からみるとかならず ＋ となります。図では第1象限にデータがプロットされます。ｘ が平均値より小さく、 ｙ が平均値より大きいケースでは第２象限にプロットされますから共分散は − の値になります。 それでは、偏差積を合計した偏差積和 Sxy がプラスであれば、何を意味するでしょうか？それは第１象限と第３象限にデータが多くプロットされていて、第２象限と、第４象限にはプロットが少ないということを示します。楕円形でいえば、右肩上がりのデータの散布状況を示すとき正の相関があるといいます。第１象限と第３象限にデータが多くプロットされていればいいので、上がり方の角度はどうでもいいのです。 第２象限と第４象限に多く分布するときは、偏差積和は−ですから負の相関があるといいます。 共分散の総和がゼロのときは無相関といいます。ただしプロット形状が楕円形や円形、長方形などの分布を示すときも共分散はゼロですから、無相関が必ずしも分布に意味がないというのは早まった判断になります。だから皆さんも散布図は必ず作って判断して下さいね。 共分散の性質でまずわかることは、その符号から座標上のデータの分布の方向が示されることです。 なお、主成分分析の理解に必要な、多次元空間での相関の正負について一般化した説明は第９章にあります。 しかし共分散にはまだ単位がありますから、共分散の数値を利用する時に比較が出来にくいのです。標準正規分布のときのように、単位によらず比較できるように数値を無次元化すればどうなるかが次の学習項目です。 因子間の関係を調べる解析分野では、いろいろな単位のある因子群を一緒に扱うと実質上解釈が出来なくなります。次節で学ぶ知識は、分散共分散行列による主成分分析があまり使われず、相関行列による主成分分析が主として使われる理由の理解につながります。

標準化共分散である、相関係数

標準化とはデータのバラツキを無次元化したものでしたね。 では、上で説明した正規分布を標準化して無次元化したときと同じ考え方で、標準化したXの偏差 と 標準化したYの偏差同士で共分散式を作れば、共分散は符号だけでなく数値までも比較できるようになるはずです。 上式は、相関係数の概念を示す式です。 　E　は期待値といって、理論値であることをさします。わかりにくければ　E{ 、｝の部分を消して考えればわかるでしょう。この式は標準化した共分散ですね。 分母に標準偏差が使われているのに注目してください。 X , Y の各データ共に標準化した値（率）で共分散（積）をつくったのが、相関係数（積率）だと言うことを示していることがわかりますね。相関係数はピアソンの積率相関係数というんですよ。 それでは、この式を変形して、皆さんご存知の相関係数の計算式にしようね。 相関係数の概念式に、それぞれ、不偏推定式を当てはめると下式のようにかくことが出来ます。 分子、分母共に　n − 1 の項があって消去されますから、皆さんおなじみの相関係数の計算式が出来上がりました。相関係数って共分散そのものということが理解できたでしょうか？ 相関係数は標準化されているから、単位のことは配慮せずに議論できますね。 相関係数は線形代数学のほうで、r =　cos θ ということが証明されていますから、次の性質があります。 その±の符号から座標上のデータの分布の方向が示される。 − 1 ≦ r ≦　1 である。 ± 1 ということは、全てのデータが、ある直線上に載っているときである。 全ての点が、直線から離れてゆき、ランダムになるにつれて、ゼロに近づいてゆく 共分散って何？と疑問を持つかたには、「簡単に言えば相関係数で教わった性質だよ」と考えれば大筋ではまちがいはありません。 ここで、単位のある共分散と、標準化して比率データにした時の共分散の違いをまとめておきましょう。 10cm の長さを mm で表すと 100 、 m で表すと 0.1 ですから情報量比は次のようになります。 　10000 : 0.01 標準化（無次元化）しなければ、この情報量の大きさで解析が進んでしまいます。mmの単位で表せば、長さの因子が大きな影響をもってしまいます。逆に m で計算するとあまり影響がないという結果になります。単位によって解釈が変わってしまいます。これが、タコ人は「主成分分析には、単位のある分散共分散からはじめるのはいけません。単位をなくして比率にした相関行列からはじめなさい」とお勧めしている理由です。   ところで皆さんは、単位のあるデータで散布図を描いた経験しかないのが普通だとおもいます。標準化したデータ同士で散布図を書くとどうなるか考えたことがありますか？ 　N( 0 , 12 )　のデータ同士の散布図では必ず傾きが 45゜の角度の散布図になります。 第4章を学んだ皆さんは、この主成分は 45゜の角度に軸がひかれることをすぐ理解できるはずです。相関係数による主成分分析を 2 因子だけで行うと、無条件で主成分軸は 45゜の角度に引かれるということを意味しています。元データから行った主成分分析では必ず 45゜になるわけではありませんね。 3因子以上の相関係数による主成分分析はこのように簡単にはなりません。 この標準化した散布図の知識は、マハラノビス汎距離の意味を理解するときや、判別分析を理解するときに必要な素養となります。 標準化データ間で散布図を作れば、データ間の距離は一般化された距離となるので、単位を考慮しなくてもよくなります。判別を判断する手続きを共通にできるのです。マハラノビス汎距離はこの標準化データ間の距離になります。

重相関係数とは

世の中には楽して好奇心いっぱいという人がいるので次のような質問が出る。 「　x　、y　の２変数の間の、相関係数はよくわかったぞ。でも世の中には、重相関係数という多変数の間で、相関係数があるらしい。すぐわかるように教えろ。」 ざっと意味を理解するだけならそれほどの問題はないよ。 重回帰分析をすると、重回帰式が求められる。このときのデータから重回帰式で算出される予測値を　Ｙｊ（データ# j= 1 , 2 ,･･････, n) とすると、観測値の yj とのあいだで、上で示したと同じ計算方法で相関係数を求めることが出来る。 このとき計算されてくる相関係数を、重相関係数といいます。簡単だったね。 ただ　0　≦ r ≦　１ と、マイナスがなくなるから気をつけてね。普通は二乗した値である決定係数として、得られた重回帰式が全情報量の何％くらい回収できるものであるかの評価に使われることが多い。

見てくれてありがとう。 ≫ 次は因子負荷量とメカニズムの関係を考えよう。  石田秀人

フレーム目次を表示