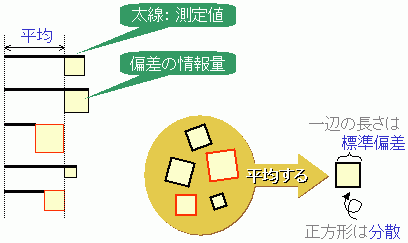
 いま、右図のように、5個の測定値の大きさを太い線分で示しています。この長さのことを効果と呼んでおきましょう。
いま、右図のように、5個の測定値の大きさを太い線分で示しています。この長さのことを効果と呼んでおきましょう。
標準偏差を計算するときに、なぜデータ個数ではなく自由度 n−1 を使うの?
そもそも自由度って何?
というご質問を受ける。
標準偏差の計算と自由度の関係がわかりにくいということで、本文にバラバラに書いてあるものを、そこだけまとめなおしてみました。
<不偏分散の公式>
平方和S 不偏分散V=━━━━━━━━ 自由度n−1不偏分散は 標準偏差 2(σ 2)の最もよい推定値になっています。偏っていないという意味で不偏と名づけられています。
|
標準偏差とは何かを知るために、まず面積の平均値を計算することからはじめよう。標準偏差とは何か (真の平均 μ で算出したとき)
標準偏差を計算する考え方はこれとおなじです。Q: いろいろな大きさの正方形があります。この平均的な面積の正方形をどうやって描けば いい? A: 全部の面積を合計して平均値を出し、その平方根を一辺とする正方形を書けばいいね。
標準偏差とは何かを知るため同じことを視覚的(四角的?)に説明しよう。
 いま、右図のように、5個の測定値の大きさを太い線分で示しています。この長さのことを効果と呼んでおきましょう。
いま、右図のように、5個の測定値の大きさを太い線分で示しています。この長さのことを効果と呼んでおきましょう。
偏差の大きさ(=個々のデータのばらつきの効果部分)を一辺とする正方形を考えます。す べてのデータは、いろいろな大きさの正方形を持っています。
効果の2乗を情報量と呼びます。
正方形の面積は2乗した値だからばらつきの情報量の値になります。
いろいろな大きさの正方 形の平均的な面積をもつ正方形が考えられますね。この平均的な正方形の面積が分散で、その ときの正方形の一辺の長さ(=ばらつきの効果)が標準偏差です。
観測データの構造
ここで学ぶことは、次の内容です。
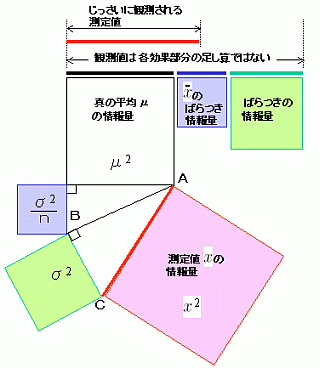
実際にフィールドで観測される測定値は、真の平均(真値)と平均値の持つばらつきと、さらにその他のばらつきとが組み合わさった値として観測されます。
次のイラストはその関係を、効果(線分の長さ)と情報量(正方形の面積)との関係として描いたものです。
イラストの説明に入る前に一般的な説明をします。
ばらつき計算や効果の計算は、情報量に変換して計算する必要があります。自然界で情報が2乗で加減算される性質を分散の加法性といいます。
もっともかんたんな事例は、 a と b という二つの効果が合わさって c という効果になるときに、
c2 = a2 + b2
となる事例ですが、数学ではピタゴラスの定理とか三平方の定理と呼んでいますね。
ではイラストの説明にはいろう。
平均値は、真の値(白)と平均値のばらつき(青)とがあわさった値ですから、右図では、ABの大きさになります。
観測データにはさらにその他のばらつき(緑)が加わりますからACのおおきさになります。すなわち赤い線分の長さが三つの情報を合わせたときの観測値(赤の線分)になるというわけです。
三つの効果部分を足し算した大きさが観測値にはならないということを学んでください。
また、通常は、観測データが先にありますから、それから平均値やバラツキを分離する情報量の配分の作業をすることがふつうに行われることです。統計とはこういう作業をすることになります。
《 知っとくと便利な知識 》 |
平方和と自由度の関係
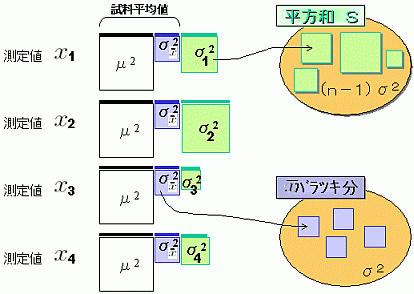
実際に実験するとき、サンプリングの仕方で、観測される平均値はばらつきます。実験して観測される平均値を試料平均値と呼びます。
すなわち試料平均値はばらつきます。しかし、真の平均値 μ はばらつきません。
このため、観測データ x は、真の平均値の情報量と試料平均の情報量とその他ばらつき情報量とに配分されます。
これをイラストで説明すれば右のようになります。
上の図と対応させて見てほしいのですが、ここでは測定値4つの情報量分解の事例が表現されています。
真値μ、試料平均値のばらつき分、および残りのばらつき部分の情報量を正方形で色分けしています。
μで平方和を計算すれば問題は無いのですが、試料平均値で計算しているので、平均値のばらつき部分(青)が、算出される平方和から抜け落ちていることを示しています。
平均値のばらつき部分は σ2/n だから、抜け落ちた情報量は全部合計するとσ 2 になります。
このことから偏りの無い分散σ 2 は自由度 n−1 で平方和を割ることで計算されることがわかります。
観測データの2乗値を合計した Σ xi2 は全情報量です。全情報量を配分すると次のようになります。
全情報量 = 真の平均値の全情報量 + 平均値のばらつき部分の全情報量 +残りの全ばらつき情報量Σ xi2 = nμ 2 + σ 2 + (n−1)σ 2
▼ 数式での説明のほうがよい人はこちら − 再クリックで閉じます
平方和Sはすべての観測データ総情報量から、試料平均の情報量を差し引いたものです。すべての測定値には真の平均が含まれていますから次式で計算できます。
ひとつの観測データについて考えると、分散の加法性から偏差dの分散は次のとおり。→(注)分散の加法性の説明は本文へ_ x = 偏差d + x
_ V [x] = V [d] + V [x ] σ 2 = V [d] + σ 2/n
V[d] = σ 2 − σ 2/n多くの観測データから算出する平方和Sは、n個の偏差の和の次式から算出される分散だから、分散の加法性よりそれぞれの偏差に上式の分散値が適用されるので
この式の意味は、試料平均値を使って平方和を計算すると、分散 σ 2 のひとつ分が足りなくなると言う意味です。y=d1 + d2 + ・・・ + dn → yの分散の期待値 V[y]=平方和 S S = V [d] + V [d] + ・・・ +V [d] = n V [d] S = nσ 2 − n( σ 2/n )= ( n − 1 )σ 2
求めたいのは真の分散 σ 2 だから、平方和Sを測定値の個数nで割ると σ 2 にはならない。求めるには( n − 1 )で割らないといけない。
( n − 1 )はこの場合の自由度ですね。
すなわち、試料平均値を用いて偏差を計算して平方和を算出すると、試料平均値がばらつきの情報量を持つために、平方和は真の平方和より σ 2 の1個分だけ、小さい値になってしまっているのです。
最初に示した不偏分散の公式は、このことを示しています。
逆に、真の平均値を用いて偏差を計算して平方和を求めた場合には、平方和は真の平方和となり nσ 2 となります。測定値の個数nで割らなければいけません。
自由度とは
統計の分野では、独立に採取された観測データ数がn個あるばあい、このデータ群は n 自由度であると表現します。
「独立に」という意味は、どの観測値も他の観測値から正確に値を決められない状態という意味です。
たとえば、観測データの中にズルをしてデータを取らず、他のいくつかのデータから計算式で算出したものがあったばあい、その観測データは他のデータから正確に値が決められます。この算出式の存在によって、自由度がひとつ減少してしまいました。ですから1自由度が減って、このデータ群の自由度は(n−1)であるということになります。
標準偏差を計算するときに、平方和Sを計算します。ここでこの意味を考えてみましょう。
この計算式には試料平均値が入っています。試料平均値はすべての観測値を合計するという算出式を使って計算されています。観測データが、
x1 〜 xn まであって合計値 T を算出すると、 xi = T − x1 − x2 − ・・・ という式に変換できますね。この合計の算出式がひとつ計算の中に入ることで、(n−1)個の観測データがあれば他のひとつの観測データは正確に値が決められる状態になります。
ですから、合計計算式の導入で、このデータ群には1自由度が減ったことになります。
すなわち、平方和の計算を行うと、そこで得られる統計量は(n−1)自由度ということになります。
これは多元連立方程式の変数がn個あれば、n個の別々の方程式がないと解が出ないということと同じですね。
たとえば、次のような x 、 y 、 z の変数を持つ方程式の値の解をだすには3つの異なる方程式が必要です。3元連立方程式でないと解は出ませんね。
2x + 3y − z = 0方程式に、 x とか y とか z が使われていますが、この式ひとつでは x , y , z に当てはまる解は無数にあります。それぞれの変数に自由度が1ずつで自由度が3。
統計の分野との対比で自由度を理解するとき、 x とか y とかであらわされる変数が統計の観測値ひとつひとつに当たります。観測値が使われた式が統計量計算に使われると自由度が減ります。
たとえば x , y , z の3観測値があるとき、自由度は3。
合計計算値を方程式のひとつとして利用すると、この式も自由度1を持っている。変数が二つになって自由度は 2。
ただしひとつの方程式に対して、任意の定数を持ってきて両辺から差し引いても自由度は3で変わらない。これは方程式の計算で、両辺から同じ数を引いても方程式は同じという性質にあたります。差し引く数が、観測値と関係のないところから適用されるため、ひとつひとつの観測値が決定されるわけではありません。
昔は平方和を手計算するときに、平均値に近い適当な数値を使って差し引いて、数字の桁数を落として計算したものです。では、適当にもってきた定数の入った計算式なら自由度はどうなるか?
観測値とは関係のない定数を差し引いても、他のどの変数も確定することはできません。だから、自由度はnのままです。
測定の対象ではあっても、真の平均値は自然の原理から得られた任意の定数で、個別の測定値を厳密に決定するものではありません。適当に持ってきた定数と同等です。
すなわち、平方和の計算のために真の平均 μ を差し引いたとしても、全く別の所から定数を持ってきたために、ひとつひとつの観測データを他の観測データから方程式で表現することはできません。自由度はn個のままなのです。
分散(σ 2)の不偏推定値は、平方和の期待値が(n−1)σ 2 である性質から自由度 (n−1)で除することで得られます。観測値の合計値を平方和の計算に使ったので、自由度が一つ減ったのです。
平均値の標準偏差
平均値にも標準偏差があるぞ。いつもでてくるから、注釈として入れておこうね。
![]()
平均値の標準偏差は 1/√n になりますから、はじめの標準偏差 σ よりばらつきが小さくなります。平均値の標準偏差が σ/√n になることを利用して平均値の差の検定などが行われることはご存知かもしれません。
100回の繰り返し測定をしたときの平均値のばらつきは 1/√100 ですから 1/10 になります。ばらつきが一桁小さくなるため、有効数字が一桁だけ向上します。もとのデータの正規分布と比較して、平均値の正規分布は 1/√n だけ狭くなっています。
この式の証明は本文にあります。また、式の誘導方法である、分散の加法性は実務的に重要な知識ですからぜひ学んでください。その事例説明も本文にあります。
本文の「ばらつきの四則演算の応用計算」をあわせて読んでもらうと分散の性質全体が見えやすいと思います。
直接ここにきた人はフレーム目次つきタコ国が全体をみわたせて便利です。ここは8章の下にあるおまけです。