Graph-R の３D バブル散布図のダウンロードと散布図作成マニュアルはこちら。
検索エンジンから直接きた方は、フレーム目次でタコ国全体がみやすいです。ここへは７章から入ります。

定量値の主成分分析の因子負荷量を解釈するときに、定量値と分類データが混在する主成分分析を体験し、トレーニングしておくと主成分分析の意味が理解できるため、かなり解釈の仕方に自信がつきます。

この章では、実際の日本食品標準成分表の主成分分析データを分類データを増減させてどのように変化するかを見てみることで、皆さんをトレーニングコーチしようというわけです。

日本食品標準成分表には、食品の性状によって穀物類とか豆類といった素材カテゴリーが決 められています。これを分類データとして使うか使わないかで、主成分分析の上でどのよう に判断が変わるかを実際にやってみよう。

なお、注意としては、ここの説明は、分散共分散行列によるものは扱わず、相関行列による主成分分析の解釈しか考慮していません。

 3つの主成分分析事例と一つの主成分層別事例を比較してみよう

• 解析１.　分析値のみの主成分分析　表１

  日本食品標準成分表の分析値のみで主成分分析する。因子負荷量行列から、因子選 択する。 因子選択の基準は、因子負荷量＞ 0.3 とし、 0.5 以上を特に強い影響をもつ因子として黄 色でマーキングする。

• 解析２． 分析値＋カテゴリ−変数　で主成分分析　表２

  上記分析値に同じ日本食品標準成分表のカテゴリーデータをダミー変数として加え たデータから主成分分析をする。

  ダミー変数に取り込んだのは、穀類、いもおよびでん粉類 、油脂類、豆類、および果実類である^（注１）。　
  解析１と同様に因子負荷量行列から、因 子選択する。解析１と解析２との比較でカテゴリーデータの取り込みの有無で主成分分析結果 がどのように変化するかを知ることができる。

• 解析３． 解析２＋１カテゴリー変数　で主成分分析　表３

  上記カテゴリーデータを加えた表にさらにもう一つ別のカテゴリーデータを入れた 場合の因子負荷量の変化を見る。付け加えたダミー変数は野菜類である。解析２と解析３の 比較でカテゴリーデータの増減はどのように主成分分析に影響するかを知ることができる。

• 解析４． カテゴリーと対応のつかない主成分（解析３から）への主成分層別　表４

  変化が生じた主成分の主成分スコアで主成分層別して何が変化の原因であるか調べる。主成分層別法の意味を理解することができる。

（注１）その他にも日本食品標準成分表には多くのカテゴリーが扱われている。その中の一部分をダミー変数に取り込んだということです。

 解析１．分析値のみのデータで得られた主成分分析

（例）　第 1 主成分の食品群は、たんぱく質が多く、糖質が少なく、ミネラル分（カルシウム、灰分、リン、カリウム）が豊富で、ビタミンのナイアシンとB2が多いという特徴をもつ。

以下、同じように各主成分について表 1 から食品の特徴が記述できますが、ここでの目標は主 成分分析の結果がどのように変化するかを見ることだから省略します。興味のある皆さんは 表1をよく見て特徴を抽出してみてください（第３章参照）。

これまでの主成分分析のやり方では、ここまでの情報取得しかできませんが、タコ国のやり 方では主成分層別法で、各主成分に属するカテゴリーと食品個別の特徴を知ることができま す。それは解析４でやってみましょう。

（注２）表を並べて比較出来るようにしているので表1、表2、表3　と横においてながめてください。

 解析２．カテゴリーデータを取り込んだ主成分分析

カテゴリーデータを取り込むことでもっと他の情報もえられています。表１と表２の比較を 行うと、選択された因子負荷量のパターンから、第１〜第５主成分までは、表１、表２とも にかなり同じデータ群が選択されてきたことが容易に推測できます^（注３）。
表２では選択されてきた主成分が２つ増えて８種類となっています。因子増加により分散が 増えて取り込まれる主成分も増えました。

新しく有効な変数が追加されたことで、データの空間散布状況に別の視点ができて新たに二つの飛び出した分布形状があることが見えたのです。

表１では第２主成分と第４主成分に交叉する分析値は２種類であったのが、カテゴリーデー タを入れると、表２のように交叉する分析値は４種類と増えてより関連が深いことを示唆し ています。表２のカテゴリー因子の選択状況でも果実類を二つとも選択しています。果実類 が二つの食品群に分かれ、果実類の特徴と果実vs油脂類の対比的な特徴をもつグループが検 出されました。果実類の空間散布状態がまがっていることと、その曲がった一方が油脂類の 散布データと対比的な位置にあることが推定できます。

こうした新規の因子の追加は、それまで同じカテゴリーと思われていたデータ群を新しく導入した因子に関係のあるデータ群とそうでないデータ群に分ける作用を持っています。
それぞれの主成分は、分析値のパターンをよく見て分類すれば、カテゴリー内でももう少し詳しい分類ができることを示しています。
たとえば第５主成分では、「脂質が多く、糖質が少なく、ビタミンCが多い」という視点で選ばれる食品のうち、果実類・脂質類の一部と対比的な穀物類の一 部があるといえます。主成分は8種類。８種類は類似の解析ができるわけですから、皆さんもやってみてください。

おや、第3主成分はカテゴリー変数が選択されてきませんでしたね。第３主成分以外の主成分は取り込んだカテゴリーデータのおかげで、どのカテゴリーの食品が、どの 主成分に関与していたのかがはっきりしてきています。たとえば、第１主成分は取り込んだカテゴリーの中では明らかに豆類の示す特徴であること がわかりますね。
「だから第３主成分は、カテゴリーとは関係が無い、分析値同士の関係である」と考えるべきでしょうか？ここで二つの可能性が出てきます。
一つは、カテゴリーとは関係なく、食品という化学物質のかたまりではどの食品でも起こる現象をキャッチしているかもしれない。
もう一つは取り上げたカテゴリー以外のその他のカテゴリーにこの特徴をもつ食品カテゴリ ーがあるというケースです。
次の解析で、カテゴリーの中で野菜類をとりあげたのですがそ れでどのように解釈すればよかったかがはっきりします。

第3主成分のようなケースの場合、「カテゴリーに関係がない」と結論しがちです。真実はどうだったのでしょうか？次の解析結果を早くみたいですね。

なるべく多くの因子を取り込んだほうが深い情報が得られていますね。

（注３）確認したければ、主成分層別法を適用すればどのカテゴリーの食品のことかははっ きりしますが、ここでは因子を一つ取り込むことが因子負荷量列にどう影響し、どのような 意味を持つのかを知りたいのでやりません。

 解析３．さらに一つカテゴリーデータを付け加えたときの主成分分析

まず最初に目に付くのは、表２の第３主成分には何もカテゴリーデータが無く所属不明の主 成分であったのが、野菜類を入れたら、第３主成分は野菜類の特徴を示した主成分であった ことが判明しました。同時にこの第３主成分（その他のカテゴリー）から野菜類が抜けて第４主成分が姿をあらわしました。
その他のカテゴリーのなかで、「カロチンとビタミンＢ１とＢ２特長を持つ一つの主成分に見えていた食品群」が二つに分裂したことを示しています。カテゴリーデータを導入したら見えなかったものが見えてきました。

右図は、変数を増加させるとみえてくるものを説明したものです。変数が２つの場合には散布図がほぼ一つの直線上になっています。ところが、もう一つの変数を加えて三次元にした場合の空間散布では2本の直線上に分かれてしまいました。
もう一つの変数が分かれる原因と何の関係も無い変数なら、変数を一つ加えたからといって空間散布が分離することはありません。このとき主成分は一つですね。
ところが変数が関係のあるものだとこのように見えなかった空間形状が見えてくるのです。この場合主成分分析をすれば主成分が一つ増加して２つになるのです。

変数が少ないと見えていないこともあるということがわかりますね。このように多変量解析のスキルを身に付ければこれまでの常識をくつがえしたり、最初から深い観察ができるのです。

こんな例で理解してもらえるかな。

君は真っ暗な洞窟に入っていった。何も見えない。
本当は目の前に岩の壁があるのに君にはわからずに、いやというほどごっつんこして目から火花を飛ばした。しかし物音にビックリしたこうもりはすいすい飛び回っている。こうもりは超音波で真っ暗でも洞窟の中が見えているのだね。

人間の目でキャッチできる情報は可視光領域の情報だけです。こうもりは人間とは別のもう一つの超音波情報を入手できます。
この場面では人間より周囲を知覚できる変数が一つ多いのです。人には何も見えないから、実際には存在する岩壁が存在しないのと同じ意味でしかありません。こうもりはもう一次元だけ情報が多いのです。人には見えなかったものがこうもりには見えています。岩は人が見えるか見えないかに関係なくそこにあるわけです。自然を理解するのに採取したデータも、肝心な変数が入っていなければ見えないわけです。

これが主成分分析で解析するとき変数を増やしておいた方がよいという理由です。

深い洞窟は人間にとっては真っ暗で恐怖の対象だけど、こうもりには怖くも何ともない超音波で照らされた明るい良く見える空間です。

主成分分析を身につけることは、真っ暗の研究領域を、灯りのついたところに変えることでもある。見えればアイデアもいろいろ湧いてきますね。
ゆっくりと勉強するだけで、君がタコから天才に変身できるかもしれません。

では、表３の第４主成分のデータ群とは何のことを言っているのでしょうか。次に、第４主成分について主成分スコアから　主成分層別法　で抽出してみましょう。

 解析４．主成分層別法の意味

この表から、第４主成分は主として豚製品の特徴を示していることが明らかになりました。解析3の経験から、獣鳥鯨肉類のカテゴリーを変数にとりこめばカテゴリー変数と関係の無かった第4主成分がその他のカテゴリーから分離するはずだね。

特に豚製品をカテゴリーデータとして主成分分析に取り込まなくても、主成分層別してしま うと、カテゴリーデータ取り込みと同じ情報にたどり着くことができました。分類型のデータであるカテゴリー変数を主成分分析に取り込むと、データマイニングしているのと同じであることがわかりますね。データを見るセンスとは関係なく層別すべきカテゴリーを先に表示してくれるのです。

分類型の変数を積極的に主成分分析に取り込むことで、解釈にあれこれ悩まずにすむので結局時間を節約できます。

あなたが取り上げたカテゴリーの中に表 3 の第４主成分のように関連するものが無かったとしても、第４主成分は分析上に何か特徴あるグループであることは保証されています。なにか必ず見出せる保証が先に示されることは、とても重要なことを意味しています。多くのデータの組の中から、特徴ある変数の性質を持つグループとしてある部分のグループが示されただけで、人間は興味を持ってそのグループの特徴を知ろうと努力し始めるのです。その場に必要な対応データが無くても対応データを探すことができる気分になれるのです。
研究者を含めて、現場をよく知っている人たちは、選ばれてきたデータのグループを一覧しただけで、ほぼ何に関係するものかは経験から予想がつくものです。そういう意味で、主成分分析と主成分層別法を組み合わせることで、現場のＱＣ７つ道具並に便利にフィールドで生じていることの発見をスピードアップしてくれるはずです。

別に技術系だけでなく、経理上こそこそ悪いことをやっている人の発見だってできるでしょうし（あまりやりたくないけど・・・）、対応のある関係の発見なら分野を問わずできるはずです。

「層別なら今やってるよ」という人はまだよく理解していません。主成分分析は、いくつかの層別因子を組み合わせた結果のほうが結果に先に出て来るのですから。たとえば、この店の水曜日の売上が他より高いという結果なら、店毎の層別でわかるのですが、主成分分析はどの他の商品との組み合わせがどの客層で特に木曜日に多いというようなことが先に結果として出してくるのです。
そして、もしカテゴリーデータが入っていない場合でも、「主成分層別法から得られるデータグループ」をよく調べることで、そのグループの特徴が因子負荷量から明らかになっているだけに関係しているカテゴリー因子が発見しやすいのです。

 

《 主成分分析を知ると論理性がわかる 》 議論の場において（あるいは言い争いの場のほうが多いかも）、一方が「あなたの意見は論理的でない」といい、もう一方が「論理的だけが真実ではない」という主張の激突が生じる。どちらも正しくどちらも正しくない。 データやグラフを出さずに言葉の論理性だけで「あなたの意見は論理的ではない」という人々の思考形態をここでは論理性優先嗜好（思考ではない）と呼んでおこう。 言葉だけでの論理展開の特徴は、多くは事例を二つにわけ、対比する言葉をあやつるか、いくつかに場合わけをするか、あるいはすべての事象は比例して直線的に増加・減少するという前提で話がなされることが多い。 実際の自然では、いくつものカーブが重なる複雑な曲線で動いている。言葉だけでの論理展開では、最適値があるとか、曲線的変化をするという場合には実態と大きく離れた結論となる。言葉は意味があいまいであり、かつ曲線的な現実を考えるには不向きである。 もう一方の「論理的だけが真実ではない」という主張は議論の場で有効な反論の材料を持たないときに逃げを打つ場合に用いられることが多い。「もっと違うことがあるんだよ（変数が足りない）」というわけである。この言い方では、あらゆることが自分の直感が正しいと主張できる。 なにやらズルいやり方のように見えるが、この「論理的だけが真実ではない」という意見がすべて間違いかというとそうでもない。データが出されたとしても、関係のないデータでは論理性の意味が消失する。 たとえば、「洞窟は暗いか」というテーマだ。目からの情報でしか動けない人間には当てはまるけれども、超音波を発信し耳で見えるこうもりにとっては「洞窟は明るい」。この例では超音波感覚というひとつの変数を外しただけで、大自然の論理は、全く逆の結論が導かれるわけである。 この変数を外す作戦は日本の官僚達が良く使う手である。問題を起こしている重要なポイントには触れないという簡単な方法で人々をだます。論理の正しさは、学識経験者であろうとなかろうと、そのテーマが論議されることでしか決めることができない。 ただ、騙されるほうがいけない。「（すべてのことを知っている）学識経験者による意見聴取した」からこの判断は間違いがない、と考えることができるのだから。 学識経験者に聞き、反対論者に発言の場を与えないというやり方は、官僚が、現実から乖離していて失敗しても、自分達に責任がこないようにして国家予算を自由に使うために、ことをうまく運ぶためにつくった仕組みである。論点を外してあいまいにすれば、議論を言語的論理性優先の世界にもちこめば黒も白と言えるし、国民の金を吸いだすあらゆることが実行可能になる実例である。 しかもやってきたことは変数外しの方法をとっているから「論理的だけが真実ではない」という言い方の立場（後者）をとっているのに、主張では学識経験者に聞いたから「この施策は論理的である」（前者）と主張できる。 これらの例で解るように、言語だけで行う「この方法は論理的である」ということと「論理的だけが真実ではない」ということには、元のデータに立ち戻らない限り、いずれも論理性は弱い。 本当に有効な施策かどうか判断するには、現実に影響を与えている変数をもれなくとらえて測定し、データの分布状態を知らなければ、現実の問題はとらえられないのだ。 「われ思う。ゆえに我あり」とは、言葉の世界の哲学で思考するといかようにも解釈できるけれど、ふと「思っている」という現実事象に立ち戻ればこの世界を揺るがぬものとして理解できることに気づいた言葉である。 主成分分析の主成分スコアの算出方法は、現実では曲線だけれども一番広がっている所の直線で考えようというやり方である。主成分分析の使い方として合成変数を作るというだけの解析では実態を直線でしか考えないから、言語的な論理性優先嗜好と同じである。 しかし少し主成分分析を深く理解すれば、元の変数のグラフを併用することで、論理性優先嗜好から現実事象に基づいた判断が出来るようになる。現実の空間散布状態を見直す主成分層別を行うことによって、現実に立ち戻れるのである。 同じ主成分分析法を使っても、その後の処理の差で、現実のとらえ方に雲泥の差が生じることに気づいていただきたい。 ＰＳ 最近の官僚達は、公聴会の記録を公開しなければいけなくなったのでＮＰＯの人々を学識経験者のなかに取り込み、反対意見を言わせて一見では公平に見える取り扱いをしている。しかし重要な変数に話が行くと、「それは重要と判断されない」と一言で議論をさえぎるやり方に変更してきている。官僚がその場で何の材料も出さずに変数の重要度を判断していいのなら公聴会など開く必要はないわけだが・・・。 世論を自分達の不利になる重要な変数に向けさせないというやり方は相変わらず不変である。江戸時代と同じ統治方式はいまだ健在。民は知らしむべからず、寄らしむべし。 Think Globally, Act Locally この言葉を Rene Dubosが言ったときは環境問題の解決に向かって発したが、今は経済界の人々が好んで使う。意味が官僚の使う意味に変化しつつ･･･。

採取データ以上のことは出てこない

関連する変数を多くすれば、主成分分析から我々が得られる情報量は増えていきます。もし関係する変数が増えればそれだけより精密で、深い情報が得られるようになります。

それは、変数を入れると、もやがかかっていた風景に風が吹き込み次々とクリアーになってゆく状況と似ています。
それと共に得られる情報としてのメカニズムや分類、対比などの精度も向上してゆきます。

あるグループの特徴を示す変数が取り込まれていれば主成分としてかならず分離されます。しかし関係の無い変数ばかりで主成分分析しても、いくら実際は特別のグループが存在していても分離されて検出されることはありません。

主成分分析は、入力データにないものを魔法で分離してくれる方法ではないということです。

多変量解析は魔法のツールではなく、やはり研究者のセンスで主成分が発見されたりされなかったりするのです。それは主成分分析が悪いのではなく、本人の自然を見る目のセンスのなさの表れなのです。

よく「主成分分析では結果が出なかったからこの方法は使えない」と真顔で言う人がいますが、恥ずかしいことだから止めよう。取り入れた変数間で常識とされる結果が主成分分析で出なかった時はデータ採取方法が不適であったはずです。

カテゴリカル主成分分析

カテゴリカル・データである分類型のデータをダミー変数として主成分分析に取り込むと、メカニズムや分類・対比などの性質を持つ主成分との関係がはっきりします。「あるメカニズムがどのカテゴリーに関連して起こっているか」とか、「対比関係にあるデータ群のどちらかにそのカテゴリーが関与している」といったような情報が得られます。
一つの主成分に複数のカテゴリー変数が選択されてくればそれはデータマイニングしていることになります。カテゴリーデータを含む主成分分析結果はデータマイニング結果そのものなのです。
カテゴリーデータを多く入れておけば、関係のある層別因子だけをひろいあげてくれるので機械的に最終の層別表を手に入れることが出来るようになりました。

（注）
カテゴリー変数を導入しようとするとすぐに多くの変数ができてしまいます。手持ちのソフトで扱える変数が小さければ（神田ソフトは２５まで）すぐにパンクしてしまいます。このような時にはカテゴリー変数を落として主成分分析した後、主成分層別を行えばダミー変数を使った解析に近い結果を得ることができます。

主成分分析の扱える変数の数が多ければ、最初からカテゴリーデータをダミー変数で取り込んで解析すればその後の解析が簡単になります。その場合でも、解析内容を自信をもって表現するためにも主成分層別を行うことを強く勧めます。主成分分析結果が出ているのに、さらに主成分層別をするのは自分を納得させる方法であり、「判断ミスをぜったい報告しないぞ」という慎重な科学的姿勢であると思います。

とりあえず変数を増やしておく

影響する変数を入れると空間散布状態をゆがませるので固有値の集中と減少ということが起こります。

定量値の変数を増やしても互いに関係が無ければ、本質的には固有値１前後の主成分ばかりになります。
どんなに変数を多くしても無相関ならば固有値1を中心にして多少の増減をするだけですから、固有値１で意味のある主成分と雑音とをよりわける方法は有効です。変数を増やしたから主成分選別の基準値を変えるということは必要ありません。
もちろん因子負荷量による変数選択の方法も無次元数であるので変数の増減で選別の基準値が変わることは無いのです。

変数を増やすことに躊躇することはありません。メカニズムには関係が無いかもしれないけれど、とりあえず変数に入れてみて計算してから考えるという方法が一番よい方法になります。
もちろん、試験データを取るにはコストがかさみますから、経済性の判断は必要になりますが、すでに実験して取得・入力済みの観測値を主成分分析に加えるという行為ならパソコンのソフトの中だけの話ですから、いくら変数を増やそうが数分の違いでしかありませんよね。

よく考えて解析せよという教えはパソコンがなく計算作業自体に大きな負担がかかっていた時代のやり方です。今はとりあえず解析してみてから考える方法も大事です。
宇宙衛星からセンサスして地球上で起こっている現象を知ろうという昨今のやり方は、とりあえず全部見てみましょうというやり方の典型です。

主成分分析法は、変数間の関係を調べるにはまず最初にとりあえずやってみる方法なのです。さらに余分なデータを除外したあとに、最後に決める手法としても使えます。

主成分分析は万能ではないが万能に使える

主成分分析は万能ではありません。それだけだと多次元空間の中で散布する点の形状の飛び出した部分や、散布した点が密集している部分を検出する方法です。

主成分スコア間の散布図、主成分層別した後の観測値間の散布図、および元データ間の散布図を作成し、重回帰分析を適用してみたり、カテゴリカルなデータマイニング表示を通じて現実をより正確に認識してゆくことができます。
適用分野ごとに、こうした解析モデルのパターンが変わるでしょう。しかし安心してください。主成分分析とは変数を合成する方法だとか、縮約する方法だとかというかたくなな理解からあなたの脳を開放してあげればいいのです。 タコ国で学んだ要素要素の知識を理解さえしておけば、ほぼすべての現実問題に対して、解析を適用できるはずです。

それでも､納得できないという方には特別の問題を出しておきましょう。

設問
２次関数の描かれた紙が多次元空間に漂っています。観測できるのは曲線だけです。これが２次関数の曲線であるということを示すにはどのようにすればよいか。

空間散布のかたまりには表面というものが有ります。曲面を持つ空間内の形状を知るためには、ノイズ処理しながらこの表面を関数化してゆく方法が必要ですし、表面の内側と外側の認識には不等式を駆使しなければいけないでしょう。
まだまだ多次元の実体認識にはこうした技術を複合する未知領域が沢山あるのです。

特に時間軸というもののなかでも順序情報は因子負荷量行列と絡み合うことでメカニズム思考を数学する方向になってゆくでしょう。

カテゴリー変数を取り込むと、分類視点が選択される分、他の解析方法より優れている性質がありますが、今の主成分分析結果は単に分類または対比情報の検出技術です。それを人間の知識と知恵を外部から補完して因子負荷量からメカニズム理解をしているわけです。主成分層別法は今のところ、その補完を可能にする一番よい方法です。
研究に必要な着想を誘発するツールとしてとても有用なものですから是非勉強してみてください。主成分分析を深く理解することができるようになるでしょう。

元のデータで３次元散布図を作って考える

コンピューターに見えている多次元空間のデータの散布状態は、3次元の空間しか理解できない我々人間にとってやはり難物だと思います。
なぜなら、こう書いている私も、一般的な主成分分析の解析方法で判断した後、レポートを書こうとしてもう一度散布図を描いてみたところ、何度も判断の基本的な考え方の部分で修正した経験があるからです。事例で示そうね。

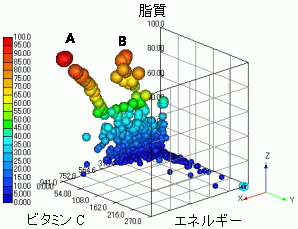
右のグラフは、3次元のバブル散布図です。日本食品標準成分表の分析値のうち、

x : エネルギー
y : ビタミン C 含量
z : 脂質含量

この３因子はあてずっぽうで選択したのではなく、主成分分析をすると同時に算出されてくる因子負荷量の大きさから機械的に選択されてきたものです。

すなわち、表 1 から第４主成分 がエネルギーと脂質とビタミンC　との関係があるよと教えてくれています。
この情報から、 x , y , z にする変数を機械的に選んだだけです。

上から見ている遠近感を表現するため Z 軸の上のほうが球の直径が大きくなっています。

さて三次元バブル散布図をよく見ると、 Ａ と Ｂ との２つの平行な別の関数関係があることがわかります。

さらに、ここでこのグラフを回転できないのが残念ですが、回転させるとＢの方はビタミンＣとの関係があり、Ａには関係ないことが読み取れます。

主成分分析でキャッチした第4主成分とは、コンピューターはＢのほうの食品グループの特徴を指摘していたわけです。主成分分析だけで議論している人は、Ａも含めて議論しますから、本当のところは知らずに議論していることになりますね。

さっそく、この二つを層別して二つを分けている要因を調べたいですよね。フリーソフト Graph-R の出番です。バブルをクリックするだけで、その元データ（X,Y,Z 値）が記録されてゆきます。これをファイルにすれば層別終わりです。すごいね。

Ａ，Ｂを層別抽出できたら、重回帰分析で、量的関係が近似式で把握できます。これだけでも報文が一つ出来ますね。

残念ながら、主成分分析結果だけからは、この情報をキャッチできなかったわけです。主成分分析の後、再び元のデータに戻って考える重要性はここにあります。主成分分析が平行な関数関係や、細かい凹凸を分離して表現してくれるわけではないのです。
また、散布図を併用しないかぎり、曲線の関数関係を発見してくれるわけでもありません。

日本食品標準成分表の結果を、この先の検討をするつもりはありませんから、どうぞどなたか検討を継続して発表して下さいね。

主成分分析を情報集約の手段として使い、「新たな指標としてこんなものが考えられる」 という程度の報告なら問題は少ないのです。しかし時代はもう少し踏み込んで、主成分分析から様々な現象のメカニズムを考える所にきています。
そこまで踏み込むと、公表する前に、少なくとも3次元レベルまでの散布図で確認を取り、自分が考えているメカニズムの内容を見直す必要があります。

そのことは、３つのメリットがあります。

1. 3次元の散布図を作って、主成分分析結果と付き合わせることで、データの分布状態の より新しい側面を発見できる。解析レベルがより深くなります。
2. 公表した後で修正するより、公表時点で深い洞察を示す方があなたの学問レベルの信頼感をより増幅してくれます。同じ手間なら、後始末より前始末。
3. 多くの場合、次に追求すべき世界が見えてきます。

カラーの３次元バブル散布図は綺麗だから、あなたの報告に眼を通してくれますよ。

３次元での解析にはほかにも、等高線図（コンター）を作成したり、カテゴリーデータなら層別散布図を作ることでかなり現実に肉薄できます。 エクセルでもすぐにできますから試してみてください。（おまけ−エクセルでの散布図作成手順）参照。

3次元バブル散布図・・・フリーソフトで手に入れる

Z方向に線分を立てる工夫も見られますが、これとて多数の点が入ると何がなにやら分からなくなります。この理由から、あまり３次元散布図は使われてきませんでした。

３次元バブル散布図は、この欠点を克服しています。人にわかりやすい俯瞰図としての空間散布状態を、あたらしい表現方法で示してくれます。

バブルとは泡。観測データの点の位置は誤差を持つわけですから、観測点から球状のある範囲で真のプロット場所があるはずです。このバブルの球半径がどれくらいが正しいかをここでは問わないこととして、バブルの陰線処理とＺ軸方向で色分けすることで、かなり複雑な形状の分布を人間が読み取ることが出来ます。

≪エクセルのバブルチャートとの違い≫

エクセルのバブルチャートは基本的には２次元の散布図です。３次元の大きさを円の直径で表す表現方法ですから、伊藤さんの３Ｄバブル散布図とは考え方が異なる表現です。
伊藤さんのものは３次元散布図です。俯瞰図で見るときに近いほうを大きく見えるようにして遠近感を表現したものです。また手前にあるバブルの向こうは陰になって見えないようにしてあります（陰線処理）。見る視点を変えられるところがすごいです。

Graph-Rの３次元バブル散布図でもバブル同士が離れてしまって、点による３次元散布図とあまり変わらない状況の散布図のときは、立体形状に言及するにはデータが少ないなあと考えてたほうがよいです。
それでもＺ軸の色情報と、３軸の回転表示を併用すると、想像で空間をうずめることくらいは出来ますから散布図を描くことは必要です。報告の中での主成分分析の結果について、断定のしかたが判断できますからね。

このグラフ表現方法は多分これから、プレゼンテーションの新しいジャンルを形成すると思います。

３次元バブル散布図は幸いなことにフリーソフトで提供されています。伊藤徹さんがつくった、 Graph-R というソフトです。
似てる名前のソフトがあるから間違えないでね。すぐにシェアウエアになるでしょうから、今が導入どきです。出来れば、今のバージョンくらいは貧乏なタコ人のためにフリーで置いておいてほしいですね。

さ・ら・に、史上初！　
エクセルでは作図できない４次元ポートフォリオ図が描けるぞ。球で表現すると迫力がおおきい。sample23.csv　を使ってやるとできます。３次元ポートフォリオ図だって可能だよ。

いろいろな種類の３次元グラフの美しいカラー表現が出来ます。グラフが回転できますから、とても有用なソフトです。
いろいろ表現形式があって、Graph-Rの作品コンテストでもしたいくらいだ。

もっとこのソフトの素敵なところがあります。バブルの一つにポインターを合わせてクリックすると、
その x , y , z の位置の数値を表示してくれます、異常値の発見とか、層別する要因の発見なんかやりやすいですね。（正確に中心を押さえないとだめ。点表示がよい）

主成分分析の利用という視点からだと、三次元バブル散布図がお勧めだけど、Graph-Rは関数式から三次元の等高線が描けたり他にも多彩な表現方式があります。グラフの見本は伊藤さんのホームページで見ることが出来ますよ。おススメ！

伊藤さん、素晴らしいソフトをありがとう。ダウンロードもここから入れます。

　 　http://www.iris.dti.ne.jp/~tohru/index.html

Graph-R の3次元バブル散布図の作成マニュアル

1. エクセルで自分のデータを3変数の一元表で入力しておく

2. GraphR178.lzh をダウンロードし、解凍して出来たフォルダー GraphR178 のなかに sample002.csv のファイルがある。通常ならエクセルのアイコンになっているはずだ。

3. Graph-R はこのsample002.csvの様式で入力していないと散布図を書いてくれないから、sample002.csv　の中に君の3変数データをコピー＆ペーストして貼り付けよう。

   君のエクセルファイルからデータ部分だけコピーし、sample002.csvの A4 の位置をフォーカスしてデータを張りつけます。前のデータがはみ出して残っているかもしれないので反転しているうちに下のほうをチェックしようね。

   エクセルの中の多くの変数から3変数を選択して貼り付ける方法は、3章のTipsに入れていますからそちらを見てね。

4. 君の好きな場所に、「名前を付けて保存」しよう。

   互換性がないけどどうする？と聞いてくるからそのまま　Yes　を選択。保存されます。 いったん、君のファイル　＊＊＊.csv　ファイルを閉じてしまおう。

5. アイコンクリックして　Graph-R　を立ち上げます。

6. とりあえずの散布図作成。

   フォルダアイコンをクリックすると　Open　で通常どおり君の保存したcsvファイルを選択をします。すぐにとりあえずの散布図が出てきます。

7. 異常値が見つかることもあるから、どの数値のことか確認してみましょう。

   右人差し指アイコンを押し込みます。この状態でいろいろな点をクリックしてみましょう。
   クリックした点のｘ、ｙ、ｚ値が、「選択データ」ウインドウに書き込まれてゆきますから、「クリップボードにコピー」すればとりあえずメモ帳などに貼り付けて、君の　＊＊＊.csv　ファイル内にある異常データ削除などの作業につなげることが出来ます。ここの「削除」ボタンはこのウインドウ数値のクリアという意味で　＊＊＊.csv　ファイルから直接データ削除することではありません。

8. 設定を変えて、3次元バブル散布図にしよう。

   白いタブつきフォルダーのデザインのアイコン「設定」を押し込みます。「設定」ウインドウが開きます。グラフの種類プルダウンメニューの▼ボタンを押すとバブル発見！バブルを選択してＯＫボタンを押します。あーら、素敵なバブル散布図に変身。

9. では散布図を回転させてみようか。

   両矢印が丸くなっている一見イヤホン風のアイコンを押し込もう。画面内の白い所でもいいから、マウスの左ボタンを押したまま、ドラッグしてみて。最初の状態に戻すには立方体マークの「位置リセットボタン」を押すだけ。楽しんでみてね。

10. デザインしようか。

    Z 軸の虹色スケールもボタンを押し込むことでいろいろ希望の位置、大きさに出来ますね。３軸方向も動かせます。画面内に文字を書き込むことは出来ません。 パワーポイントなどに貼り付けて軸の凡例を文字で入れ込む場所を想定してデザインしてみてください。

11. 2次元散布図にする。

    となりのXYアイコンなど希望のものを押せばよいです。

12. 画像保存する。

    画像保存ボタンで pngファイルや jpgファイルに保存できます。
    他の方法として、一般に Windows では、ALT ＋ PrintScreen でフォーカスされているウインドウのイメージをクリップボードにコピーします。これをPhotoshopや、PowerPoint、IrfanView（フリー、お勧め）などのソフトに貼り付けてファイルにする方法を覚えておくと便利です。貼り付け方法はドローソフトを立ち上げてから Ctrl ＋ V 。

13. 等高線図など他の表現にはsample00＊.csvの ＊ の番号を選択することでおこなわれます。

14. エクセルを使わずに、添付されている Sample002.csv ファイルに入力して、入力シートをCtrl+Aでシートごとクリップボードにコピーすると、GraphーRの「ファイル」からクリップボード渡しもできます。