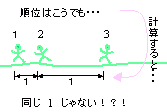
 順位データには1位と2位、2位と3位の間で等間隔性がありません。例えば小学校のさくら組の時の1位2位はダントツで1位で入ったのに、うめ組の1位と2位は接戦でほとんど同時に入ったとします。1と2の間で等間隔じゃないだろ? 順位データには1位と2位、2位と3位の間で等間隔性がありません。例えば小学校のさくら組の時の1位2位はダントツで1位で入ったのに、うめ組の1位と2位は接戦でほとんど同時に入ったとします。1と2の間で等間隔じゃないだろ?順位データについては他にもあるぞ。順位は1番からしか勘定しない。このことが平均値の扱いに注意をすべき性質になっている。 事例から先に考えようね。次の例は統計上の扱いのどこに誤りがあるか?考えてみて。
- ある学校で養護教室の子供3人がかけっこをして順位を決めました。他の教室は50人全員が一度にはしり、順位を決めました。双方の平均値を計算して養護教室の生徒の平均値が低いから、かけっこの能力は養護教室の生徒の方が高いという結論をだしました。
- 20m走でオリンピックの選手10人の順位平均と、幼稚園児の10人の順位平均が同じなのでオリンピックの選手も、幼稚園児も能力的に同じである。
主成分分析では順位に連動して動く相関を扱うから、順位データの平均値にまつわる問題は出ませんね。どんどん使って下さいね。格付けの場合でも数値の評価は各自直感で適当につけているのが実情だよね。
格付けでも数値の決め方で平均値が変わってしまいますから、平均値比較などは、意味があるかないかは十分考えて行うように。説明しても間違った使い方をする人がよくいるからなあ。 統計学をかじった先生の中には、こういう尺度論を持ち出して適用してはいけないとか言いがちです。しかし、計算を前提に作業しているのなら、世の中の全ての順序データや格付けデータを使っている手法は全て否定されるべきなのです。
でも、全ての統計を教える先生は尺度の話とは別に、官能検査の解析方法では順位や格付けの数値で計算しています。安心して使っていいよ。 しかし、小学生の集団で 1 番と、オリンピック選手の 1 番は早さが違う。こうした数値を同じ数値 1 として計算の中でとりあつかって計算した結果に何の意味があるかがわからなくなる。こうした矛盾をなんとか回避するためには、限度見本とか、順位判断の技術的な判断基準を作るのが普通だ。比較してはいけないものをあらかじめ排除すようにするんだよ。 順位や格付けデータはどうあがいても「完全なる等間隔性」なんて保証できないのが普通だから、最後はこうした基準をエイヤッと決めるしかないけどね。それでも全くないときよりは、測定した日にちが違ってもある程度の比較できる数値にはなっているはずだから、科学の領域に入ってくるはずだよ。 尺度の等間隔性などの問題は、解析をやってはいけないという問題ではなく、解析結果の報告時に結論に断定的な言葉を使わないとか、そういう配慮をすることになります。
かえって不安になるから詳しく説明するね。 数値に等間隔性が保証されないと、計算して足したり引いたりしても、結果にどんな意味があるか分かりません。りんご2つ足したら、1個以下になりましたって話はないもんね。
え?実際にそういう事例はあるよ。
姫リンゴ2つの重量は、りんごの富士1個よりはるかに小さい。日常でそういう比較をしないのは、君達の頭の中で、大きい種類のりんごと小さい種類のりんごは重量で比較してはいけないと限度見本ができてるんだ。
りんごだとできるのに、なぜ会社の仕事だと出来なくなるんだろうね。不思議!
それから、日本の気温とアメリカの気温の測り方は摂氏と華氏との違いがあって、そのままの数値で一緒に計算しても結果は何のことやらわからなくなるよね。これは摂氏0度と華氏0度は違う場所で0度となっているからなんだ。さらに1度の差も違うから計算するにはどちらかに換算しなければならないんだ。 間隔尺度の取り扱いはこういうスケール差や原点である0ポイントの差を考慮しないと計算できないんだ。僕達は計算するときに日常あまり意識しないで、こうした換算活動をしているんだよ。
質量なんかは0ポイントがはっきりしているけれど、トンで計ったりポンドで計るなど単位の違いがあると、同じ物でも数値は変わってくるよね。
しかしこれは、分母に同じ単位のもので比率にすれば、世界中どんな単位のデータであっても、同じ数値になってしまうんだ。工学系の人たちは無次元化なんていってるよね。これは比率尺度で話をしようということなのです。
一般論で厳密な数学を目指すときには、このようなことを配慮して理論構築することが必要だよ。
でも我々の現実社会では、天気を予測するのに、「あの山の右側に灰色の雲が出たら、午後は雨だよ」程度のことを分かるのも重要なことです。 分類データである「あの山」であるかどうか、「何色の雲か」程度が変数として重要なんだ。主成分分析は尺度の制限がなくてよい手法だし、多次元の散布状態のひろがり方向を扱っているので、大まかな因子間の関連を見るには最適な手法なんだ。
対比的に変化しているグループの発見や、メカニズムの発見に、主成分分析を使おうとしているのだから、ここでは名義尺度、順位尺度、格付け尺度も積極的に使っていきます。実際のビジネスの場ではお金をとってむしろ積極的にこのような尺度が使われています。
本当に統計を知っている神様の先生達はそういう初心者いじめをしたりしないものです。 「タコ人よ!強くあれ!」
格付けのやり方も書いとくね。組織にいるとタコ以下の上司達がいて、情報は精密であればあるほどよいと主張するアホがいます。 人間も味覚や聴覚、視覚などのセンサーとして測定するとやはり識別能力の限界があることが分かってるんだ。だから、調査用紙にどんなに詳細な段階の質問項目を入れてもかえって調査精度がおちるよ。 例えば、極上上旨、極上旨、極上やや旨、極上やや下旨、超上旨・・・(以下極下下マズまで続く)などと回答用紙に入れてみても、普通の人はやや旨いとかややまずい程度を選択する。 しかし世の中には変な奴が必ずいるから、極上上でも足らないなど回答する奴がいる。数値で処理するとなると、普通の人が±2前後で回答するときに、こいつらは±10などという数値で回答する。数値的に5倍の強度(5人分の意見となる)があるから、全体の評価はこいつらの評価に大きく引きずられてしまうんだ。 結果として、一般の人の評価とは大きくずれた精度の悪いものになる。
もっとも、異常な奴らを調査するときにはいいかも。
人間のセンサーとしての能力から何段階を判断できるかという数値を示しておくね(佐藤信、官能検査入門)。感度の良い人でもこれに±1を付け加える程度まで。人間は目で多くの情報処理していることがわかるね。
あ、それからこの識別能力と人間にたいしての重要性とは全く次元の違う話だからね。
味覚: 4段階(食塩水の濃度差)
聴覚: 5段階(音の大きさ)
視覚:10段階(2点のマーカー識別)
嗅覚も味覚や聴覚レベルだと推定されます。しかし、人間は同じ味の濃度だけでなくいろいろな味の質を区別できているし、ひとつひとつはあまり感度のよくないセンサーを組み合わせてより多様な区別が出来る能力を持っています。だから、数値的な調査だけでなく、調査対象の人々が言う「咲きかけの朝露の中でにおうバラのかおり」等という表現には意味があるので、統計調査ばかりに拘泥しないように。 それから人を分析機械として使うときには、ゼロ合わせ・スパンあわせのための訓練が必要となります。訓練した人達は分析パネリストと呼ばれ一定の嗜好傾向が出てきますので、いくら感度がよくても今度は一般の社会の人の嗜好調査には向きません。 付け足しになるけど、多少かじったことのある人への注意。
重回帰分析も同じ入力方式でダミー変数を使うけれど、機械が8台の場合なら変数はひとつへって7つになっているから、主成分分析に使用したデータを重回帰分析に流用するときは注意が必要だよ。そのまま使っちゃダメ。このことは第5章で説明するね。
|