（おまけ） 早わかり　主成分分析　

主成分分析は英語では ＰＣＡ: Principal Components Analysis といいます。

主成分分析だけだと、それは主成分スコアの計算方法です。
一般に言葉では次のように説明されます。すべて同じことの説明です。

• 説明変量の圧縮
• 多変数から少数の総合的指標にする
• 多変数から少数の合成変数にする
• データの低次元化
• データの圧縮または縮約
• 情報の簡素化・要約

＜主成分分析で行うこと＞

 

これまで 主成分スコアの計算 これから 多変数から複数のメカニズムの分離（主成分スコアの計算と同じ。利用目的が異なる） メカニズム提示（因子負荷量と相関方向） 主成分回帰（単純な曲線の重回帰） メカニズムの曲線方程式の算出（主成分層別によるメカニズム関連データ抽出と重回帰による方程式）

■　主成分分析とは

主成分スコアとはなんだろうか？

多次元の空間でも同じです。データの点々が散布しているとき、平均値を中心にして、全部の軸をグルグル回転させていちばん広がっているところで軸を決めてゆく計算をしているだけです。軸はすべて直交しています。

詳細は第4章で説明

詳細な行列計算を知らなくても主成分分析の解釈は可能です。

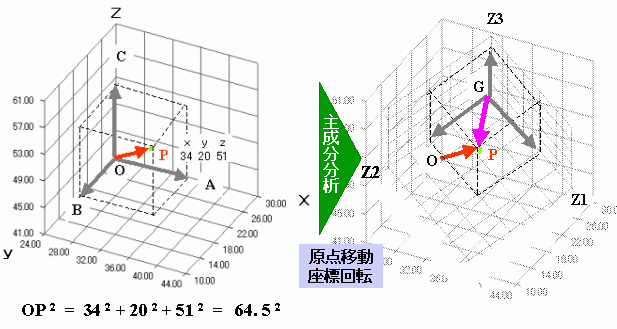
次の図は点　P（ x ､ y ､ z ）＝ P（ 34 ､ 20 ､ 51 ）の座標位置を示しています。

ＯＰ（赤矢印）がこのデータの全情報量で、64.5²の大きさを持っています。この情報を　x 、y ､ z のそれぞれの情報量に配分すると
　x² ＝ 34² 　（ＯＡ）、  y² ＝ 20² 　（ＯＢ）、  z² ＝ 51²　（ＯＣ）となります。

主成分分析をすると図では右のようになり、原点Ｏが変数の平均値である重心Ｇに移動します。

さらに点Ｐも含めた全体の散布点において一番広がっている方向に軸が回転して移動します。新しく出来た回転後の軸 Z₁ ､ Z₂ ､ Z₃ が主成分軸です。

そして、ＧＰを新しい座標軸に射像した値（右図グレーの矢印）が点Ｐの主成分スコアになります。

各主成分スコアの計算は、はじめに観測した変数 x ､ y ､ z 　の関数式から計算されます。そのため、関数式の x ､ y ､ z に係数が掛かりますが、 Z₁ 軸の射影値が求まるように係数の値が決まります。その係数が固有ベクトルです。すなわち、それぞれの対応する変数の固有ベクトル値と対応する変数値と掛け算して全部足し合わせたものが主成分スコアとなります。係数値は主成分計算したら自動的にプリントアウトされてきます。

この主成分スコア計算の意味するところは、「新しい総合指標を求める」ということです。一番広がったところに主成分直線を描くという性質によるものです。

《ちょっと知っているといい話》

主成分分析は平均値同士の比較は行っていない

主成分スコアで研究結果を論議するときに必要な注意点があります。ＯＰ（赤）がＧＰ（ピンク）になったとき、平均値の情報量は抜き取られてしまいます。だから主成分分析は平均値比較は行っておらず、変化量どうしの関係を見ていることになります。研究報告などでは平均値比較情報として観測データ間の散布図は必ず入れて、考察に加える必要があります。

主成分分析はばらつきを考慮している

一般の統計解析方法は、正規分布のパラメーターである平均値と偏差の性質を利用して平均値効果とばらつき効果を分離しています。これを情報量の配分といいます。
主成分分析は単に軸の回転と射影で情報量の再配分をするだけですから、様々な尺度のデータを混用しても理論的には何の問題もありません。 主成分分析は射影が個別のベクトルのばらつき効果そのものとなります。
だから一般に議論されているように、「主成分分析にはばらつきが考慮されていない」という主張は、理解不足ということになります。

主成分分析はどんなふうに使われてきたのだろうか？

• 主成分スコアは新しい指標づくりに使われてきました。
  たとえばアンケート結果から主成分スコアを計算して顧客満足度を計算する、などという使い方がされてきました。

• 多変量のデータから可視化したマップをつくることにも使われてきました。
  「いろいろな技術の現在の状況を視覚化してサイエンスマップをつくりたい」とか、「顧客嗜 好のポートフォリオを作りたい」という希望は主成分スコアの計算をして、主成分スコア同士の散布図を作ることだけでかないます。

• 画像処理などにもつかわれています。
  低解像度のデジカメ画像のいくつかの周辺色情報から拡大した隙間の部分の色調を 決定して、ギザギザを防ぎ自然な画像にするなどというときに使われます。

今後、どんな風に使われるのだろうか？

次の図は、主成分分析の利用のしかたがどのように違うかを図示したものです。もとの観測データにもどってそのメカニズムを考えようという思想の違いを示しています。

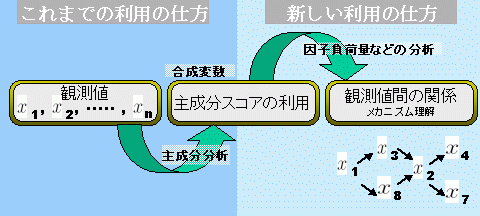
主成分分析を主成分スコアの計算方法とだけ考えるやり方は、古い考え方です。大学の授業な ら主成分分析法の計算方法だけ教えればよいので、こうした説明で十分です。しかし現実の社会の中で主成分分析を応用する場では、こうした理解だけでは不十分です。

• 人間の遺伝子も解明されて、現在では多数の遺伝子情報から関連するものを抽出しメカニズム を抽出する必要がでてきています
• 多くの分析値が一度にどっと吐き出される分析装置もかなり実用段階にきています
• 経済でも、証券界でも、ネットで調査されるアンケートなどコンピューターがはきだすデータは毎年膨大になってきています
• 医学でも、立体的な画像情報と症例のデータが多量に蓄積されてきています。この蓄積データからミスなく、リアルタイムに因果関係を引き出したいという希望は多くなってきています

数学オンチを自認する皆さんがどのように参加してゆけるのでしょうか？

実測される観測データ群から、スイッチ、ポンで、これまで世の中にない概念も主成分スコアとして計算されてきます。これまで世の中にない概念も算出できるため、直接測定できないような新しい指標を求める心理学、経済、経営などの分野で多用されてきました。

それは、対数の計算方法は知らなくても、関数電卓の logキー ひとつで対数値が計算できる感覚です。

すなわち、主成分スコアがどのような意味を持つかを知りさえすれば、主成分分析結果は行列 式の計算の意味など理解しなくても主成分分析は使えるわけです。だからこのサイト、タコ国では主成分分析の計算式などは記載していません。主成分スコアの計算方法なら、他のサイトに詳しく書いてありますからそちらを参照なさってくださいね。

身の回りにあるあらゆることで因果関係のある事象を、数値的に証明するといったことが考えられます。また、起こっている現象を分類してしまうこともできます。データマイニングなんて主成分分析で機械的に出来ることです。

このタコ国で説明する新しい主成分分析の使用方法はもとの観測データにもどって考えるやりかたですから、これまでのグラフや表の作成方法で対処できます ♪

トップへ　

■　次世代の主成分分析の利用法とは

次世代はこんなことに使われる

メカニズム提示

同時に算出されてくる因子負荷量（主成分負荷量という人もいる）を手がかりにして、実測さ れる変数間の因果関係（メカニズム）を抽出できます。

メカニズムの分離

数種のメカニズムが混合している場合に、メカニズムも個別に分離してくれます。

変数選択

あるメカニズムに関係のない変数と関係のある変数をよりわけることができます。

データマイニング指針提示

層別データとか分類型のデータはカテゴリカルデータと呼ばれています。主成分分析にカテゴ リカルデータを取り入れると、多くの変数の中から層別すべきカテゴリカル変数だけを選択し てくれます。

やりかたの事例詳細は第3章で説明

しかし、主成分分析は万能ではありません。メカニズムが直線関係にあるという条件のもとで しか、こうしたことはできません。これまで主成分分析を利用してきた人は、こうしたことを 知っていても知らなくても利用してきたわけですから、社会では、こうした前提を受け入れて います。

というより、むしろ魔法の多変量解析だからコンピューターが計算した結果に誤りはないとい う信じ方で運用されてきたきらいがあります。人間の心理過程は決して直線ではないですし、 経済だって、規模の限界から来る頭打ちがありますから直線関係はありえません。

主成分分析だけですべてを済ませようとすること自体、より正確に現実の出来事を理解するに は不十分です。
しかし、主成分分析を行った後に、その結果といくつかの他の手法を組み合わせることによって、主成分分析法は見違えるほどすばらしいデータ解析方法に生まれ変わります。

トップへ　  　 

■　主成分スコア計算後の分析方法とは

主成分スコアの計算をしたあとに行う解析とはどのようなことをするのでしょうか？

1. とりあえず選択された変数間の元データでの散布図を描く

   主成分分析後に、因子負荷量（主成分負荷量ともいいます）から選択されてきた変数間の2次元散布図を、無処理の元のデータ間で表示させて確認することはとても重要です。

   何を確認するかというと次のようなことです。

   • データの散布状態には関数関係がみられそうか？
   • 全体に均等にばらついていないか？
   • 散布状態は直線とみなしてよいか？
   • グループに分かれる散布状態ではないか？
   • 平行な直線が存在しないか？
   • 元データで判断した相関の正負と主成分に関して因子負荷量から結論される相関の正負が一致するか？
   • 決定的に結論できるほど散布点（測定数）はあるか？

   佐藤の３次元バブル散布図（フリーソフト）なら、見やすい位置に自由に回転表示できるため、さらに次のようなことを判断できます。

   • 平面状か？中身の詰まった散布状況か？
   • 最適値や最大値、最小値などはどの数値の組み合わせあたりか？

   確認事項のそれぞれが何を言おうとしているかわからない人は本文を勉強してください。少なくとも主成分分析で学会発表レベルの仕事をするつもりなら、間違った考察をして恥をかかないために必要です。科学者として大自然と真正面に向き合うために必要です。

    

2. 主成分スコアどうしの散布図を作成する方法

   主成分分析後に、必ず行う必要がある作業が、主成分スコアどうしの散布図作成です。この作業の中から、まず行いたいのが関数関係の有無の判断です。

   関数関係がありそうであれば、主成分スコアを用いた回帰分析をおこないます。変数の次数や対数、逆数、または交互作用の有無の判断は、散布図から人間が判断します。

   しかし、実際に観測されるデータ群では、主成分スコアだけから関数関係を見出せることは少ないため、次のような工夫をします。

    

3. 最初の観測値を各主成分の特徴のあるものに分類してしまうという方法

   
   

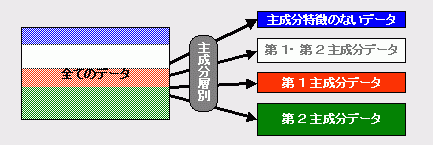
   たとえば第1主成分のデータだけを抜き出してしまえば、以降の解析は今まで皆さんが行ってきたグラフ作成などのやり方で解析できます。

   一般に使われているグラフや表などの集計ででてきた結果はそのまま第1主成分の性質ということになります。さらに回帰分析で第1主成分だけの方程式を作ることもできますね。

   データ層別の方法は二つ提案されています。

   • 相関方向の点対称象限に存在する観測値を抽出する
   • 主成分スコアの限界値を設定して割り振る。通常は標準正規分布の±σ点（６８％基準）を限界点とする

   主成分層別法

   相関係数をもとに計算した主成分スコアなら、数値の大小でその主成分に関係するデータかどうかを選択することができます。その主成分で考えずに、その他の主成分の影響が強いデータを排除してゆけばよいのです。

   具体的な方法は、第３章に説明しています。エクセルでの主成分層別マクロの紹介もしていますから、煩雑な分類とソートはデータのはりつけ作業をすればエクセルで行えます。
   選別の基準は ±σ の範囲以外にあれば、その主成分の影響が強いと判断する方法をとります 。もちろん、いろいろな選別の基準が考えられますし、解析結果の使用目的にあった基準がこ れからもいろいろ出てくると思います。皆さんもチャレンジできる分野です。

   主成分層別法の限界については第４章や第７章に記載しています。

   おなじみのグラフや表類

   主成分分析でデータを主成分ごとにより分けて、もとのデータ間の関係に戻すのですからこれまで使ってきたあらゆるグラフ類が利用されます。プレゼンテーションにも相手にわかりやすい状態に加工されていることが特徴になります。

    

4. 変数を選択してメカニズムを抽出するという方法

   主成分軸の存在する象限（相関方向）は因子負荷量の符号の正負に一致します。相関係数の正負の解釈を、多次元に拡大して解釈できます。

   相関方向分析法

   相関方向分析法は主成分の示すメカニズムの意味を因子負荷量から誘導するときに必要な知識であり根拠です。だからメカニズムを決定するためにつかわれます。
   相関方向分析法は、従来では２変数の相関の正負で表現されていた概念を、多次元の変数に拡 張した概念です。相関を正負であらわすことができるのは２次元までですから、拡張表現を新しくつくらなければなりません。タコ国では第９章に説明しています。
   主成分分析では直線でしか考えませんが、相関方向分析では曲線の扱いも可能です。そのため 、人間がひとまとまりの関係と考えた空間内のデータ抽出に利用できます。 計算そのものは、データと平均値の大小をコンピューターで象限ごとに選別させるだけの簡単なものです。

   重回帰分析法

   相関方向分析法あるいは主成分層別法で抽出されたデータ群の曲線を方程式にします。詳細は第５章で説明
   層別を行わない場合には。主成分回帰法となります。

   回帰分析が理解しやすいため主成分分析法より身近で、手法自体は重回帰分析法のほうが人気があります。
   主成分分析で選択された変数（因子）群を使って重回帰分析をします。重回帰分析による変数選択法は、多重共線性という計算上の制約から、重要な変数から消してゆくという性質がありますので本質的な変数選択法ではありません。「関係のある」という言葉を排除して、「排除できるだけ排除して元の情報をできるだけかき集める」変数選択法であるということを知って いなければいけません。

トップへ　 

 本文に戻る

検索エンジンから直接ここにきた人はフレーム目次つきタコ国が全体をみわたせて便利です。ここは第４章の下にある（おまけ）です。